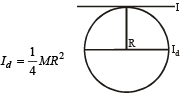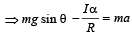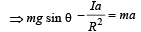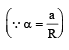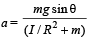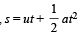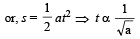31 Year NEET Previous Year Questions: System of Particles & Rotational Motion - 3 - NEET MCQ
30 Questions MCQ Test - 31 Year NEET Previous Year Questions: System of Particles & Rotational Motion - 3
A ring of mass m and radius r rotates about an axis passing through its centre and perpendicular to its plane with angular velocity ω. Its kinetic energy is [1988]
A solid homogeneous sphere of mass M and radius R is moving on a rough horizontal surface, partly rolling and partly sliding. During this kind of motion of the sphere [1988]
A solid cylinder of mass m and radius R rolls down an inclined plane of height h without slipping. The speed of its centre of mass when it reaches the bottom is [1989]
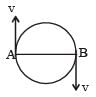
A particle of mass m is moving in a horizontal circle of radius R with uniform speed v. When it moves from one point to a diametrically opposite point, its [1989]
Moment of inertia of a uniform circular disc about a diameter is I. Its moment of inertia about an axis ⊥ to its plane and passing through a point on its rim will be [1990]
The moment of inertia of a body about a given axis is 1.2 kg m2. Initially, the body is at rest. In order to produce a rotational kinetic energy of 1500 joule, an angular acceleration of 25 radian/sec2 must be applied about that axis for a duration of [1990]
A fly wheel rotating about a fixed axis has a kinetic energy of 360 joule when its angular speed is 30 radian/sec. The moment of inertia of the wheel about the axis of rotation is [1990]
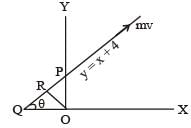
A particle of mass m = 5 is moving with a uniform speed  in t h e XOY pl ane al o ng the line y = x + 4. The magnitude of the angular momentum of the particle about the origin is [1991]
in t h e XOY pl ane al o ng the line y = x + 4. The magnitude of the angular momentum of the particle about the origin is [1991]
If a sphere is rolling , the ratio of the translational energy to total kinetic energy is given by [1991]
The speed of a homogenous solid sphere after rolling down an inclined plane of vertical height h from rest without sliding is [1992]
A solid sphere, disc and solid cylinder all of the same mass and made of the same material are allowed to roll down (from rest ) on the inclined plane, then [1993]
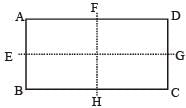
In a rectangle ABCD (BC = 2 AB). The moment of inertia is minimum along axis through [1993]
Angular momentum is [1994]
A spherical ball rolls on a table without slipping.Then the fraction of its total energy associated with rotation is [1994]
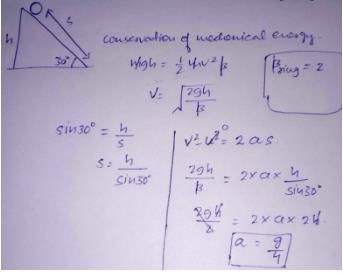
A thin uniform circular ring is rolling down an inclined plane of inclination 30° without slipping.
Its linear acceleration along the inclination plane will be [1994]
The angular speed of an engine wheel making 90 revolutions per minute is [1995]
Two racing cars of masses m and 4m are moving in circles of radii r and 2r respectively. If their speeds are such that each makes a complete circle in the same time, then the ratio of the angular speeds of the first to the second car is [1995]
The ABC is a triangular plate of uniform thickness. The sides are in the ratio shown in the figure. IAB, IBC and ICA are the moments of inertia of the piate about AB, BC and CA respectively. Which one of the following relations is correct ? [1995]
If a flywheel makes 120 revolutions/minute, then its angular speed will be [1996]
The angular momentum of a body with mass (m), moment of inertia (I) and angular velocity (ω) rad/sec is equal to [1996]
A couple produces [1997]
The centre of mass of a system of particles does not depend upon [1997]
In carbon monoxide molecule, the carbon and the oxygen atoms are separated by a distance 1.12 × 10–10 m. The distance of the centre of mass, from the carbon atom is [1997]
A thin circular ring of mass M and radius r is rotating about its axis with a constant angular velocity ω. Two objects each of mass m are attached gently to the opposite ends of a diameter of the ring.The ring will now rotate with an angular velocity [1998]
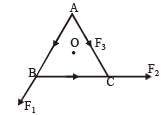
O is the centre of an equilateral triangle ABC. F1, F2 and F3 are three forces acting along the sides AB, BC and AC as shown here. What should be the magnitude of F3, so that the total torque about O is zero? [1998]
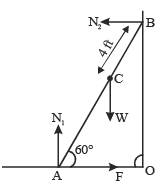
A weightless ladder 20 ft long rests against a frictionless wall at an angle of 60º from the horizontal. A 150 pound man is 4 ft from the top of the ladder. A horizontal force is needed to keep it from slipping. Choose the correct magnitude of the force from the following
Two racing cars of masses m1 and m2 are moving in circles of radii r1 and r2 respectively. Their speeds are such that each makes a complete circle in the same time t. The ratio of the angular speeds of the first to the second car is [1999]
The moment of inertia of a disc of mass M and radius R about an axis, which is tangential to the circumference of the disc and parallel to its diameter, is [1999]
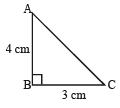
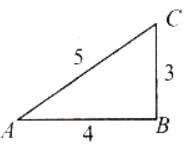
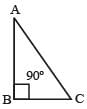
There is a flat uniform triangular plate ABC such that AB = 4 cm, BC = 3 cm and angle ABC = 90º.The moment of inertia of the plate about AB, BC and CA as axis is respectively I1, I2 and I3. Which one of the following is true? [2000]
A solid cylinder and a hollow cylinder both of the same mass and same external diameter are released from the same height at the same time on an inclined plane. Both roll down without slipping. Which one will reach the bottom first? [2000]


 and for ring I = mr2
and for ring I = mr2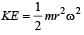

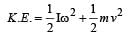
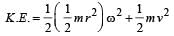
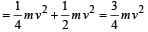
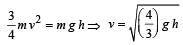

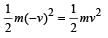
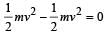
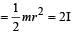
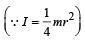
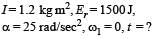
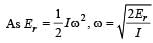
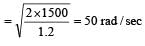
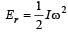
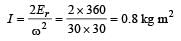
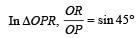
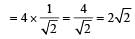
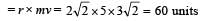

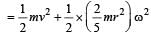
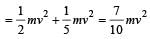
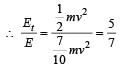
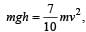
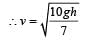
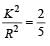
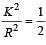
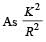 for solid sphere is smallest, it takesminimum time to reach the bottom of the incline
for solid sphere is smallest, it takesminimum time to reach the bottom of the incline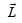 is defined as
is defined as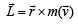
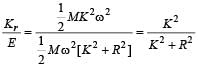
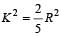
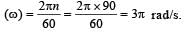
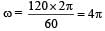 rad/sec
rad/sec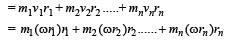
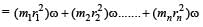
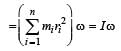
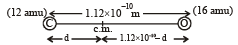

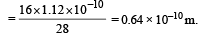
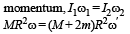
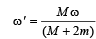
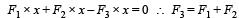
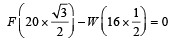
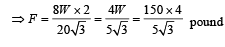
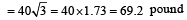
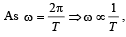 as T is same in both
as T is same in both