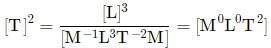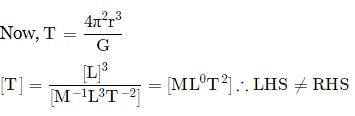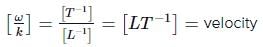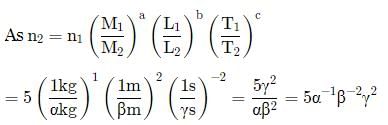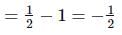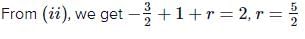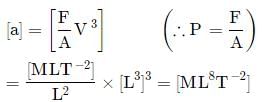Test: Dimensional Analysis & Its Applications (NCERT) - NEET MCQ
10 Questions MCQ Test - Test: Dimensional Analysis & Its Applications (NCERT)
Checking the correctness of equations using the method of dimensions is based on
Using the principle of homogeneity of dimensions, which of the following is correct?
Which of the following relations is dimensionally incorrect?
Which of the following relations for the displacement of a particle undergoing simple harmonic motion is not correct dimensionally?
The displacement of a progressive wave is represented by y = A sin(ωt - kx) where x is distance and t is time. The dimensions of ω/k are same as those of the
If velocity of light c, Planck's constant h and gravitational constant G are taken as fundamental quantities then the dimensions of length will be:
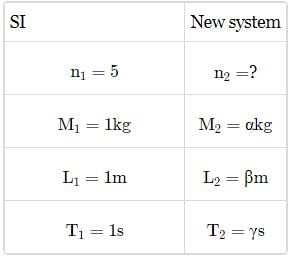
A new system of units is proposed in which unit of mass is α kg, unit of length is β m and unit of time is γ s. What will be value of 5 J in this new system?
If the energy, E = Gp hq cr where G is the universal gravitational constant, h is the Planck's constant and c is the velocity of light, then the values o f p, q and r are, respectively
The equation of state of a gas is given by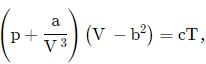 where p,V,T are pressure, volume and temperature respectively and a,b,c are constants. The dimensions of a and b are respectively
where p,V,T are pressure, volume and temperature respectively and a,b,c are constants. The dimensions of a and b are respectively
The velocity of a particle (v) at an instant t is given by v = at + bt2. The dimension of b is the