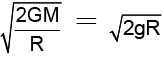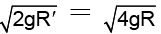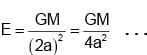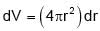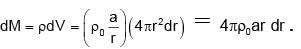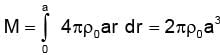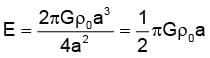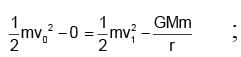Test: Gravitation - NEET MCQ
25 Questions MCQ Test - Test: Gravitation
The height above surface of earth where the value of gravitational acceleration is one fourth of that at surface, will be
The decrease in the value of g on going to a height R/2 above the earth's surface will be
If the rotational motion of earth increases, then the weight of the body -
On doubling the distance between two masses the gravitational force between them will -
If the acceleration due to gravity inside the earth is to be kept constant, then the relation between the density d and the distance r from the centre of earth will be -
Let w be the angular velocity of the earth's rotation about its axis. Assume that the acceleration due to gravity on the earth's surface has the same value at the equator and the poles. An object weighed at the equator gives the same reading as a reading taken at a depth d below earth's surface at a pole (d << R). The value of d is
The mass and diameter of a planet are twice those of earth. What will be the period of oscillation of a pendulum on this planet if it is a seconds pendulum on earth ?
If the kinetic energy of a satellite orbiting around the earth is doubled then -
The escape velocity from a planet is v0. The escape velocity from a planet having twice the radius but same density will be -
Two planets A and B have the same material density. If the radius of A is twice that of B, then the ratio of the escape velocity is
A hollow spherical shell is compressed to half its radius. The gravitational potential at the centre
A satellite of the earth is revolving in circular orbit with a uniform velocity V. If the gravitational force suddenly disappears, the satellite will
Two point masses of mass 4m and m respectively separated by d distance are revolving under mutual force of attraction. Ratio of their kinetic energies will be
The figure shows variation with energy with the orbit radius of a body in circular planetary motion. Find the correct statement about the
curves A, B and C
A body of mass m rises to height h = R/5 from the earth's surface, where R is earth's radius. If g is acceleration due to gravity at earth's surface, the increase in potential energy is
A planet has mass 1/10 of that of earth, while radius is 1/3 that of earth. If a person can throw a stone on earth surface to a height of 90m, then he will be able to throw the stone on that planet to a height
A body of mass m is situated at a distance 4Re above the earth's surface, where Re is the radius of earth. How much minimum energy be given to the body so that it may escape -
A satellite of earth is moving in its orbit with a constant speed v. If the gravity of earth suddenly vanishes, then this satellite will -
The ratio of distances of satellites A and B from the centre of the earth is 1.4 : 1, then the ratio of energies of satellites B and A will be –
The distance between earth and moon is 4 × 105 km and the mass of earth is 81 times the mass of moon. Find the position (take 104 km as unit) of a point on the line joining the centres of earth and moon, where the gravitational field is zero.
If the radius and density of a planet are two times and half respectively of those of earth, find the intensity of gravitational field at planet surface and escape velocity from planet.
The density inside an isolated large solid sphere of radius a = 4 km is given by ρ = ρ₀a / r, where ρ₀ is the density at the surface and equals to 109 kg/m3 and r denotes the distance from the centre. Find the gravitational field (in m/s2) due to this sphere at a distance 2a from its centre. Take G = 6.65 × 10–11 Nm2/kg2.
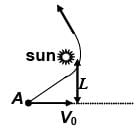
A cosmic body A moves towards star with velocity v0 (when far from the star) and aiming parameter L and arm of velocity vector v0 relative to the centre of the star as shown in figure. Find the minimum distance (take 108 m as unit) by which this body will get to the star. Mass of the star is M.
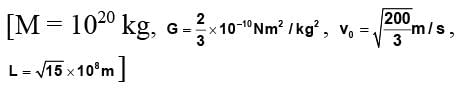
A person brings a mass of 1 kg from infinity to a point A. Initially the mass was at rest but it moves at a speed of 2 m/s as it reaches A. The work done by the person on the mass is –3J. The potential at infinity is –10 J. Then find the potential at A.


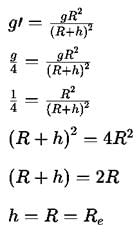



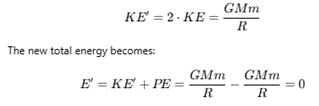
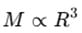
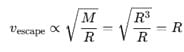
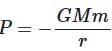
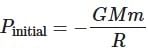
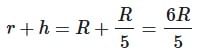
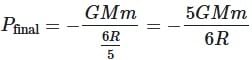

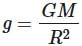
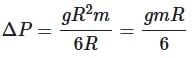
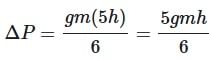

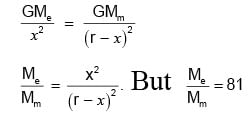
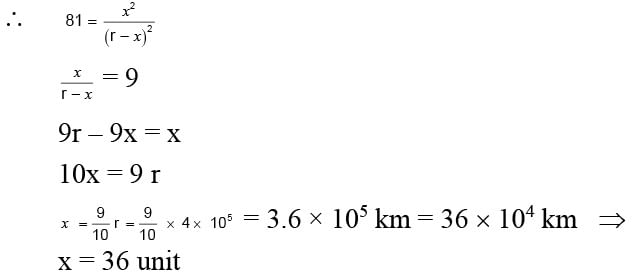
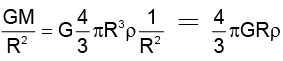
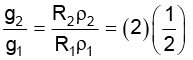 = 1 ∴ g2 = g1 = g
= 1 ∴ g2 = g1 = g