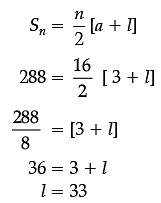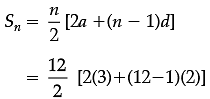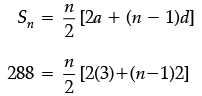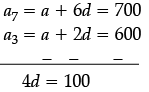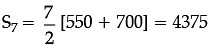Case Based Questions Test: Arithmetic Progressions - CAT MCQ
15 Questions MCQ Test Additional Study Material for CAT - Case Based Questions Test: Arithmetic Progressions
Read the following text and answer the following questions on the basis of the same: Amit has a packet of Candies. It consists of 288 candies. He arranges the candies in a way that first row contains 3 candies, second row has 5 and third row has 7 and so on.There are a total 16 rows.
Q. How many candies are there in the last row?
Read the following text and answer the following questions on the basis of the same: Amit has a packet of Candies. It consists of 288 candies. He arranges the candies in a way that first row contains 3 candies, second row has 5 and third row has 7 and so on.
Q. If Amit want to make 12 rows, then how many total candies will be placed by him with same arrangement.
Read the following text and answer the following questions on the basis of the same: Amit has a packet of Candies. It consists of 288 candies. He arranges the candies in a way that first row contains 3 candies, second row has 5 and third row has 7 and so on.
Q. How many rows are there?
Read the following text and answer the following questions on the basis of the same: Amit has a packet of Candies. It consists of 288 candies. He arranges the candies in a way that first row contains 3 candies, second row has 5 and third row has 7 and so on.
Q. Find the difference in the candies placed in the 10th and 15th row.
Read the following text and answer the following questions on the basis of the same: Amit has a packet of Candies. It consists of 288 candies. He arranges the candies in a way that first row contains 3 candies, second row has 5 and third row has 7 and so on.
Q. Is there any row which contains 28 candies?
Read the following text and answer the following questions on the basis of the same: In a potato race, a bucket is placed at the starting point, which is 5 m from the first potato and the other potatoes are placed 3 m apart in a straight line. There are ten potatoes in the line (see figures).
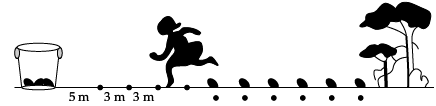
A competitor starts from the bucket, picks up the nearest potato, runs back with it, drops it in the bucket, runs back to pick up the next potato, runs to the bucket to drop it in, and she continues in the same way until all the potatoes are dropped in the bucket.
Q. What is the distance run to pick up the 2nd potato?Read the following text and answer the following questions on the basis of the same: In a potato race, a bucket is placed at the starting point, which is 5 m from the first potato and the other potatoes are placed 3 m apart in a straight line. There are ten potatoes in the line (see figures).
A competitor starts from the bucket, picks up the nearest potato, runs back with it, drops it in the bucket, runs back to pick up the next potato, runs to the bucket to drop it in, and she continues in the same way until all the potatoes are dropped in the bucket.
Q. What is the distance run to pick up the 4th potato?
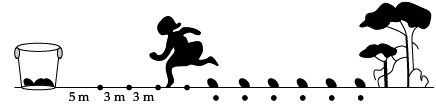
Read the following text and answer the following questions on the basis of the same: In a potato race, a bucket is placed at the starting point, which is 5 m from the first potato and the other potatoes are placed 3 m apart in a straight line. There are ten potatoes in the line (see figures).
A competitor starts from the bucket, picks up the nearest potato, runs back with it, drops it in the bucket, runs back to pick up the next potato, runs to the bucket to drop it in, and she continues in the same way until all the potatoes are dropped in the bucket.
Q. What is distance run to pick up the 1st potato?
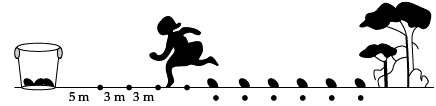
Read the following text and answer the following questions on the basis of the same: In a potato race, a bucket is placed at the starting point, which is 5 m from the first potato and the other potatoes are placed 3 m apart in a straight line. There are ten potatoes in the line (see figures).
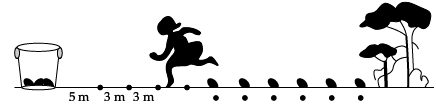
A competitor starts from the bucket, picks up the nearest potato, runs back with it, drops it in the bucket, runs back to pick up the next potato, runs to the bucket to drop it in, and she continues in the same way until all the potatoes are dropped in the bucket.
Q. What is the distance run to pick up the 3rd potato?Read the following text and answer the following questions on the basis of the same: In a potato race, a bucket is placed at the starting point, which is 5 m from the first potato and the other potatoes are placed 3 m apart in a straight line. There are ten potatoes in the line (see figures).

A competitor starts from the bucket, picks up the nearest potato, runs back with it, drops it in the bucket, runs back to pick up the next potato, runs to the bucket to drop it in, and she continues in the same way until all the potatoes are dropped in the bucket.
Q. What is the total distance run by the competitor?Read the following text and answer the following questions.
A manufacturer of TV sets produced 600 sets in the third year and 700 sets in the seventh year, assuming that the production increases uniformly by a fixed number every year.
Q. Find the production in the 10th year.
Read the following text and answer the following questions.
A manufacturer of TV sets produced 600 sets in the third year and 700 sets in the seventh year, assuming that the production increases uniformly by a fixed number every year.
Q. What is the difference between the productions of two consecutive years?
Read the following text and answer the following questions.
A manufacturer of TV sets produced 600 sets in the third year and 700 sets in the seventh year, assuming that the production increases uniformly by a fixed number every year.
Q. Find the production in the first year?
Read the following text and answer the following questions.
A manufacturer of TV sets produced 600 sets in the third year and 700 sets in the seventh year, assuming that the production increases uniformly by a fixed number every year.
Q. Find the total production in the first 7 years.
Read the following text and answer the following questions.
A manufacturer of TV sets produced 600 sets in the third year and 700 sets in the seventh year, assuming that the production increases uniformly by a fixed number every year.
Q. If they produced 600 sets in the year 2010. Then in what years their production will be 1000?
|
5 videos|378 docs|164 tests
|