RD Sharma Test: Real Numbers - 2 - Class 10 MCQ
25 Questions MCQ Test Mathematics (Maths) Class 10 - RD Sharma Test: Real Numbers - 2
Find the largest number which divides 62,132,237 to leave the same reminder
The product of two numbers is -20/9. If one of the numbers is 4, find the other.
For some integer m, every odd integer is of the form
If 112 = q×6+r, then the possible values of r are:
The largest number of 4 digits exactly divisible by 12, 15, 18 and 27 is
On a morning walk, three persons step off together and their steps measure 40 cm, 42 cm and 45 cm, respectively. What is the minimum distance each should walk so that each can cover the same distance in complete steps?
Pairs of natural numbers whose least common multiple is 78 and the greatest common divisor is 13 are:
The largest number which divides 70 and 125, leaving remainders 5 and 8, respectively, is
If A = 2n + 13, B = n + 7, where n is a natural number then HCF of A and B is:
The LCM of two number is 45 times their HCF. If one of the numbers is 125 and the sum of HCF and LCM is 1150, the other number is:
The difference of a rational and an irrational number is always
If n is a rational number, then 52n − 22n is divisible by
The relationship between HCF and LCM of two natural numbers is
|
127 videos|550 docs|75 tests
|




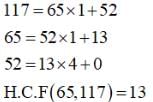
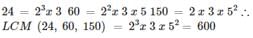
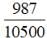 will have
will have