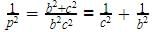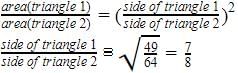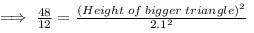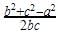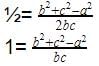RS Aggarwal Test: Triangles - Class 10 MCQ
25 Questions MCQ Test Mathematics (Maths) Class 10 - RS Aggarwal Test: Triangles
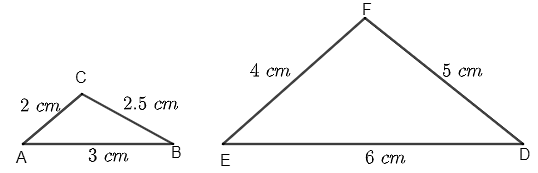
Triangle ABC is such that AB = 3 cm, BC = 2 cm and CA = 2.5 cm. Triangle DEF is similar to ΔABC. If EF = 4 cm, then the perimeter of ΔDEF is :
In ΔABC, AB = 3 cm, AC = 4 cm and AD is the bisector of ∠A. Then, BD : DC is :
ABC is a triangle and DE is drawn parallel to BC cutting the other sides at D and E. If AB = 3.6 cm, AC = 2.4 cm and AD = 2.1 cm, then AE is equal to :
The line segments joining the mid points of the sides of a triangle form four triangles each of which is :
In ΔABC and ΔDEF, ∠A = 50°, ∠B = 70°, ∠C = 60°, ∠D = 60°, ∠E = 70°, ∠F = 50°, then ΔABC is similar to:
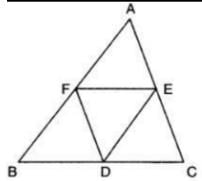
D, E, F are the mid points of the sides BC, CA and AB respectively of ΔABC. Then ΔDEF is congruent to triangle
If in the triangles ABC and DEF, angle A is equal to angle E, both are equal to 40°, AB : ED = AC : EF and angle F is 65°, then angle B is :-
In a right angled ΔABC, right angled at A, if AD ⊥ BC such that AD = p, If BC = a, CA = b and AB = c, then:
In the adjoining figure, XY is parallel to AC. If XY divides the triangle into equal parts, then the value of AX/AB =
The ratio of the corresponding sides of two similar triangles is 1 : 3. The ratio of their corresponding heights is :
The areas of two similar triangles are 49 cm2 and 64 cm2 respectively. The ratio of their corresponding sides is:
The areas of two similar triangles are 12 cm2 and 48 cm2. If the height of the smaller one is 2.1 cm, then the corresponding height of the bigger one is:
In a triangle ABC, if AB, BC and AC are the three sides of the triangle, then which of the statements is necessarily true?
The sides of a triangle are 12 cm, 8 cm and 6 cm respectively, the triangle is :
In an equilateral triangle, the incentre, circumcentre, orthocentre and centroid are:
In the adjoining figure D is the midpoint of BC of a ΔABC. DM and DN are the perpendiculars on AB and AC respectively and DM = DN, then the ΔABC is :
Triangle ABC is such that AB = 9 cm, BC = 6 cm, AC = 7.5 cm. Triangle ΔDEF is similar to ABC, If EF = 12 cm then DE is :
In ΔABC, AB = 5 cm, AC = 7 cm. If AD is the angle bisector of ∠A. Then BD : CD is:
In a ΔABC, D is the mid-point of BC and E is mid-point of AD, BF passes through E. What is the ratio of AF : FC?
The difference between altitude and base of a right angled triangle is 17 cm and its hypotenuse is 25 cm. What is the sum of the base and altitude of the triangle is ?
If AB, BC and AC be the three sides of a triangle ABC, which one of the following is true?
In the adjoining figure D, E and F are the mid-points of the sides BC, AC and AB respectively. ΔDEF is congruent to triangle :
In the adjoining figure ∠BAC = 60° and BC = a, AC = b and AB = c, then :
|
126 videos|457 docs|75 tests
|