Test: Problems on Pythagoras Theorem - Grade 10 MCQ
10 Questions MCQ Test - Test: Problems on Pythagoras Theorem
The monitors of computers are measured along the diagonal. What is the size of the largest monitor that can be placed in a space measuring 17″ x 21″?
If the legs of an isosceles right triangle are 5 cm long, approximate the length of the hypotenuse to the nearest whole number.
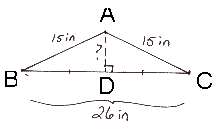
Find the height of the given triangle if its base is 26 inches and the slant side is 15 inches long as shown below.
If the sum of the squares of a and b is the same as the square of c and if m < n, then for what value of k can the Pythagorean triples be generated with the following equations?
a = n2 + k , b = 2mn : c = m2 + n2
Find the total perimeter of the given figure.
What is the diagonal length of a TV screen whose dimensions are 80 cm x 60 cm?
If the sum of the length of the legs of a right triangle is 49 cm and the hypotenuse is 41 cm, find its shortest side.
How far up a wall will an 11m ladder reach, if the foot of the ladder is 4m away from the wall?
A wood frame for pouring concrete has an interior perimeter of 14 metres. Its length is one metre greater than its width. The frame is to be braced with twelve-gauge steel cross-wires. Assuming an extra half-metre of wire is used at either end of a cross-wire for anchoring, what length of wire should be cut for each brace?
Anuj swims across a pool diagonally every day. The pool is 4 m wide, and it is 16 m diagonally across. What is the length of the pool?