Test: Number System- Assertion & Reason Type Questions - Class 8 MCQ
10 Questions MCQ Test Advance Learner Course: Mathematics (Maths) Class 8 - Test: Number System- Assertion & Reason Type Questions
DIRECTION : In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : 5 is a rational number.
Reason : The square roots of all positive integers are irrationals.
DIRECTION : In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : Sum of two irrational numbers is an irrational number.
Reason : Sum of a rational number and an irrational numbers is always an irrational number.
DIRECTION : In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : 78 ፥ 74 = 74
Reason : If a > 0 be a real number and p and q be rational numbers. Then ap x aq = ap + q.
DIRECTION : In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : √5 is an irrational number.
Reason : A number is called irrational, if it cannot be written in the form p/q, where p and q are integers and q ≠ 0.
DIRECTION : In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : The rationalizing factor of 3 + 2√5 is 3 – 2√5.
Reason : If the product of two irrational numbers is rational then each one is called the rationalising factor of the other.
DIRECTION : In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : Rational number lying between two rational numbers x and y is
½ (x + y).
Reason : There is one rational number lying between any two rational numbers.
DIRECTION : In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : Sum of two irrational numbers 2 + √3 and 4 + √3 is irrational number.
Reason : Sum of two irrational numbers is always an irrational number.
DIRECTION : In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : 113 x 114 = 1112
Reason : If a > 0 be a real number and p and q be rational numbers.
Then ap x aq = ap + q.
DIRECTION : In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Q. Assertion : Rational number lying between 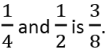
Reason : Rational number lying between two rational numbers x and y is ½(x y).
DIRECTION : In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : 0.329 is a terminating decimal.
Reason : A decimal in which a digit or a set of digits is repeated periodically, is called a repeating, or a recurring, decimal.
|
5 videos|57 docs|20 tests
|
|
5 videos|57 docs|20 tests
|



















