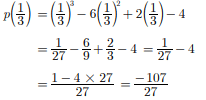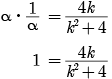Test: Polynomials- Assertion & Reason Type Questions- 2
14 Questions MCQ Test Mathematics (Maths) Class 9 | Test: Polynomials- Assertion & Reason Type Questions- 2
| 1 Crore+ students have signed up on EduRev. Have you? |
Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : The sum and product of the zeros of a quadratic polynomial are 
respectively.
Then the quadratic polynomial is 4x2 +x+1.
Reason : The quadratic polynomial whose sum and product of zeros are given is x2-(sum of zeros). x + product of zeros.
respectively.Sum of zeros 
product of zeros = 1/4
Quadratic polynomial be 
Quadratic polynomial be 4x2 +x + 1. So, both A and R are correct and R explains A.
Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : If (x + 1) is a factor of f(x) = x2 + ax + 2, then a = - 3.
Reason : If (x - a) is a factor of p (x), if p (a) = 0.
Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : If both zeros of the quadratic polynomial x2 - 2kx + 2 are equal in magnitude but opposite in sign then value of k is 1/2.
Reason : Sum of zeros of a quadratic polynomial ax2 + bx + c is b/a
sum of zeros = 0
Assertion (A) is false but reason (R) is true.
Thus (d) is correct option.
Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : x3 + x has only one real zero.
Reason : A polynomial of nth degree must have n real zeroes.
Again, x3 +x = x(x2 + 1)
which has only one real zero
(x = 0) [x2 + 1 ≠ 0 for all x ε R]
Assertion is true.
Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : The remainder when p(x) = x3 - 6x2 + 2x - 4 is divided by (3x - 1) is -107/27.
Reason : If a polynomial p(x) is divided by ax - b , the remainder is the value of p(x) at x = b/a.
p(x) = x3 - 6x2 + 2x - 4
Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : P(x) = 14x3 - 2x2 + 8x4 + 7x - 8 is a polynomial of degree 3.
Reason : The highest power of x in the polynomial p(x) is the degree of the polynomial.
= 14x3 - 2x2 + 8x4 + 7x - 8 is 4.
Degree of p(x) is 4. So, A is incorrect but R is correct.
Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : (x + 2) is a factor of x3 + 3x2 + 5x + 6 and of 2x + 4.
Reason : If p(x) be a polynomial of degree greater than or equal to one, then (x - a) is a factor of p(x), if p(a) = 0
g(x) = x + 2
x = -2
put x = -2 in p(x)
p(-2) = (-2)3 + 3(-2)2 + 5(-2) + 6
= -8 + 12 - 10 + 6
= 0
since p(x) is zero
X + 2 is a factor of x3 + 3x2 + 5x + 6
Checking
let x = -2 q(x) = 2x + 4
q(-2) = 2(-2) + 4
= -4 + 4
= 0
since reminder is zero
x + 2 is a factor of 2x + 4
Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : If one zero of poly-nominal p(x) = (k2 + 4)x2 + 13x + 4k is reciprocal of other, then k = 2.
Reason : If (x - α) is a factor of p(x), then p(α) = 0
i.e. α is a zero of p(x).
Let α, 1/α be the zeroes of p(x), then
k2 - 4k + 4 = 0
(k - 2)2 = 0
k = 2
Assertion is true Since, Reason is not correct for Assertion.
Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : The expression 3x4 - 4x3/2 + x2 = 2 is not a polynomial because the term -4x3/2 contains a rational power of x.
Reason : The highest exponent in various terms of an algebraic expression in one variable is called its degree.
Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : x2 + 4x + 5 has two zeroes.
Reason : A quadratic polynomial can have at the most two zeroes.
Assertion
Consider the given polynomial x2 + 4x + 5
Because the degree of the polynomial is 2. It is a quadratic polynomial.
We know that the quadratic polynomial has at the most two zeroes.
∴ x2 + 4x + 5 has two zeroes.
∴ Assertion is true.
Reason Clearly, Reason is true.
Since both the Assertion and Reason are true and Reason is a correct explanation of Assertion.
Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : 3x2 + x - 1 = (x + 1) (3x - 2) + 1.
Reason : If p(x) and g(x) are two polynomials such that degree of p(x) ≥ degree of g(x) and g(x) ≥ 0 then we can find polynomials q(x) and r(x) such that p(x) = g(x) q(x) + r (x), where r(x) = 0 of degree of r(x) < degree of g(x).
If g(x) is any polynomial then it can divide p(x) by q(x) where 0 < q(x) and may get a remainder say r(x).
If g(x) perfectly divides p(x) by q(x), then r(x) = 0.
It is obvious that deg r(x) < deg g(x).
∴ we can find polynomial q(x) and r(x) such that
p(x) = q(x)q(x) + r(x), where r(x) = 0 or deg r(x) < deg g(x)
Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : (x + 2) and (x - 1) are factors of the polynomial x4 + x3 + 2x2 + 4x - 8.
Reason : For a polynomial p(x) of degree ≥ 1, x - a is a factor of the polynomial p(x) if and only if p(a) ≥ 1.
p(x) = x4 + x3 + 2x2 + 4x - 8
p(-2) = (-2)4 + (-2)3 + 2(-2)2 + 4 (-2) - 8
= 16 - 8 + 8 - 8 - 8 = 0
So, (x + 2) is a factor of p(x).
p(1) = (1)4 + (1)3 + 2(1)2 + 4(1) - 8
= 1 + 1 + 2 + 4 - 8 = 0
(x - 1) is a factor of p(x).
Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : (2 - √3) is one zero of the quadratic polynomial then other zero will be (2 + √3).
Reason : Irrational zeros (roots) always occurs in pairs.
Direction: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion : If f(x) = 3x7 - 4x6 + x + 9 is a polynomial, then its degree is 7.
Reason : Degree of a polynomial is the highest power of the variable in it.
|
88 videos|397 docs|109 tests
|
|
Use Code STAYHOME200 and get INR 200 additional OFF
|
Use Coupon Code |
|
88 videos|397 docs|109 tests
|
Download free EduRev App
Related content with Test: Polynomials- Assertion & Reason Type Questions- 2
|
|
|
Related tests with Test: Polynomials- Assertion & Reason Type Questions- 2
|
|
|
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
