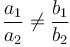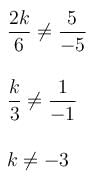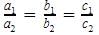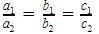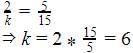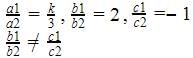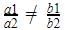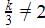Practice Test: Pair of Linear Equations in Two Variables - Class 10 MCQ
15 Questions MCQ Test Mathematics (Maths) Class 10 - Practice Test: Pair of Linear Equations in Two Variables
The pair of linear equations 2kx + 5y = 7, 6x – 5y = 11 has a unique solution if
The pair of equations 3x + 4y = k, 9x + 12y = 6 has infinitely many solutions if –
The pair of linear equations 2x + 5y = k, kx + 15y = 18 has infinitely many solutions if –
The pair of linear equations 3x + 5y = 3, 6x + ky = 8 do not have any solution if –
The pair of linear equations 3x + 7y = k, 12x + 2ky = 4k + 1 do not have any solution if
8 girls and 12 boys can finish work in 10 days while 6 girls and 8 boys can finish it in 14 days. Find the time taken by the one girl alone that by one boy alone to finish the work.
The pair of linear equations kx + 4y = 5, 3x + 2y = 5 is consistent only when –
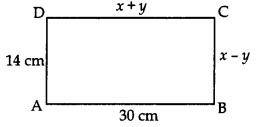
In Fig., ABCD is a rectangle. Find the values of x and y.
Three chairs and two tables cost Rs. 1850. Five chairs and three tables cost Rs. 2850. Then the total cost of one chair and one table is –
Six years hence a man's age will be three times the age of his son and three years ago he was nine times as old as his son. The present age of the man is –
The solution of the equations x - y = 2 and x + y = 4 is:
The pairs of equations 9x + 3y + 12 = 0 and 18x + 6y + 26 = 0 have
The pairs of equations x + 2y - 5 = 0 and -4x - 8y + 20 = 0 have:
If the lines 3x + 2ky – 2 = 0 and 2x + 5y + 1 = 0 are parallel, then what is the value of k?
If one equation of a pair of dependent linear equations is -3x + 5y - 2 = 0. The second equation will be:
|
129 videos|736 docs|84 tests
|