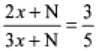Important Questions Test: Ratio & Proportion- 2 - UPSC MCQ
15 Questions MCQ Test CSAT Preparation - Important Questions Test: Ratio & Proportion- 2
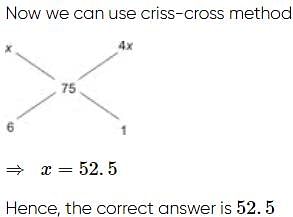
What is the angle in degrees made by a sector, the ratio of whose area with the area of the semicircle is equal to 1:10?
The value of a diamond varies directly as the square of its weight. If a diamond worth Rs 10,000 is divided into 2 pieces in the ratio of 4:6, what is the loss in value?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The first, second and third class fares between two railway stations, Patna and Lucknow were 10:8:3 and the number of first, second and third class passengers between the two stations was is 3:4:10. If total sales of the ticket is Rs 16,100, find the money obtained by the sales of second class tickets.
Two horses cost as much as 5 dogs, 6 dogs as much as 8 oxen, 10 oxen as much as 50 sheep, 14 sheep as much as 9 goats. If the price of one goat is Rs 70, how much will one horse cost?
A is proportional to B. B is inversely proportional to C. C is proportional to the square of D. D is directly proportional to the cube root of E. Assuming positive integers, if A increases then E
The sum of four numbers is 253. The ratio of the first number to the second number is 2:3. The ratio of the second number to the third number is 5:6. The ratio of the third number to the fourth number is 8:9. What is the average of the second number and the third number?
A man has rs.480 in the denominations of one-rupee notes, five-rupee notes and ten-rupee notes. The number of notes of each denomination is equal. What is the total number of notes that he has ?
Three friends A, B and C started a venture with capitals in the ratio of 4:1:15. At the end of every quarter A halves his capital, while B doubles his capital and C leaves his capital untouched. This process is repeated till the end of the year. If at the end of the year B ’ s share of the profit is Rs 22,000, what is the total profit?
Gandhiji owns cows, some black and some white. He finds that 4 black cows and 3 white cows gave the same amount of milk in 5 days as 3 black cows and 5 white cows gave in 4 days. What is the ratio of milk given by a black cow in a day to that given by a white cow in a day?
A metal trader buys 2 kinds of silver foils, the ratio of their prices being 1:4. He sells the alloy at Rs 90 per kg so that he can make a profit of 20%. If the ratio of their quantities present in a alloy is 6:1 respectively, find the purchase price of the foil present in lesser quantity.
Read the passage below and solve the questions based on it.
A book having pages between 4,000 and 5,000 is divided into four parts, each part being divided into chapters. The total number of pages in each of the four parts is the same. The ratio of the chapters across all the parts is 6:5:10:14. The number of chapters in the fourth part is 70
Q.What is the total number of pages in the book?
The ratio of the age of Sita and her mother is 2:3. N years from now, ratio of their ages will become 3:5. What is the value of N?
P works twice as fast as Q, whereas P and Q together can work three times as fast as R. If P, Q and R together work on a job, in what ratio should they share the earnings?
Read the passage below and solve the questions based on it.
There are certain number of apples, guavas and oranges in a basket. The number of each variety is more than one. The ratio of the number of apples to the number of guavas is equal to the ratio of the number of guavas to the number of oranges.
Q.
If the total number of fruits is 61, then find the number of guavas.
A man has 25 paise, 50 paise and 1 Rupee coins. There are 220 coins in all and the total amount is 160. If there are thrice as many 1 Rupee coins as there are 25 paise coins, then what is the number of 50 paise coins?
|
218 videos|139 docs|151 tests
|