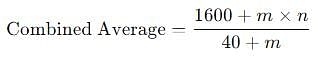Practice Test: Averages - 1 - UPSC MCQ
15 Questions MCQ Test CSAT Preparation - Practice Test: Averages - 1
The average of a batsman after 25 innings was 56 runs per innings. If after the 26th inning his average increased by 2 runs, then what was his score in the 26th inning?
There are 7 members in a family whose average age is 25 years. Ram who is 12 years old is the second youngest in the family. Find the average age of the family in years just before Ram was born?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The average weight of a class of 10 students is increased by 2 kg when one student of 30kg left and another student joined. After a few months, this new student left and another student joined whose weight was 10 less than the student who left now. What is the difference between the final and initial averages?
The average of 15 numbers is 18. If each number is multiplied by 9, then the average of the new set of numbers is:
The average number of runs scored by Virat Kohli in four matches is 48. In the fifth match, Kohli scores some runs such that his average now becomes 60. In the 6th innings he scores 12 runs more than his fifth innings and now the average of his last five innings becomes 78. How many runs did he score in his first innings? (He does not remain not out in any of the innings)
Dev and Om are among 22 students who write an examination. Dev scores 82.5. The average score of the 21 students other than Om is 62. The average score of all the 22 students is one more than the average score of the 21 students other than Dev. The score of Om is.
The average marks of a group of 20 students on a test is reduced by 4 when the topper who scored 90 marks is replaced by a new student. How many marks did the new student have?
The average weight of 3 boys Ross, Joey and Chandler is 74 kg. Another boy David joins the group and the average now becomes 70 kg. If another boy Eric, whose weight is 3 kg more than that of David, replaces Ross then the average weight of Joey, Chandler, David and Eric becomes 75 kg. The weight of Ross is:
The mean temperature of Monday to Wednesday was 35 °C and of Tuesday to Thursday was 30 °C. If the temperature on Thursday was 1/2 that of Monday, the temperature on Thursday was ______ .
The average age of a family of 5 members is 20 years. If the age of the youngest member is 10 years, what was the average age of the family at the birth of the youngest member?
The average weight of 10 men is decreased by 2 kg when one of them weighing 140 kg is replaced by another person. Find the weight of the new person.
The average age of a group of men is increased by 6 years when a person aged 26 years is replaced by a new person of aged 56 years. How many men are there in the group?
The average weight of a class is 54 kg. A student, whose weight is 145 kg, joined the class and the average weight of the class now becomes a prime number less than 72. Find the total number of students in the class now.
Consider a class of 40 students whose average weight is 40 kgs. m new students join this class whose average weight is n kgs. If it is known that m + n = 50, what is the maximum possible average weight of the class now?
|
218 videos|139 docs|151 tests
|