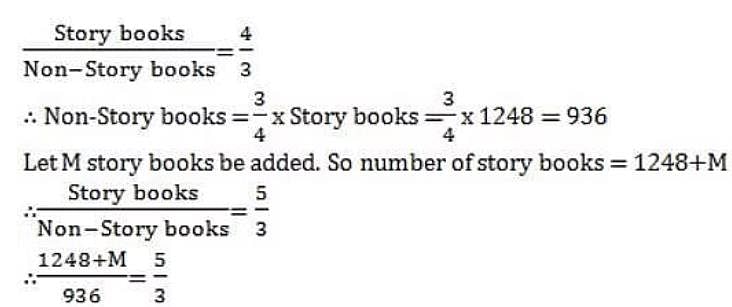Practice Test: Ratio & Proportion- 1 - UPSC MCQ
10 Questions MCQ Test CSAT Preparation - Practice Test: Ratio & Proportion- 1
If the work done by p men in (p + 2) days is to the work done by (p + 4) men in (p – 1) days is in the ratio 1 : 1, then the value of p is:
If A is 25% less than B, then what will be the value of (2B - A)/A ?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The monthly incomes of X and Y are in the ratio of 4:3 and their monthly expenses are in the ratio of 3:2. However, each saves Rs. 6,000 per month. What is their total monthly income?
The incomes of Sheldon, Leonard, and Howard are in the ratio of 4 : 5 : 6 respectively and their spending are in the ratio of 6 : 7 : 8 respectively. If Sheldon saves one fourth his income, then the savings of Sheldon, Leonard, and Howard are in the ratio:
A sum of Rs. 12,384 is divided between A, B, C and D such that the ratio of the shares of A and B is 3 : 4, that of B and C is 5 : 6, and that of C and D is 8 : 9. What is the share of C ?
In a library, the ratio of number of story books to that of non-story books was 4:3 and total number of story books was 1248. When some more story books were bought, the ratio became 5:3. Find the number of story books bought.
There are three persons A, B and C in a room. If a person D joins the room, the average weight of the persons in the room reduces by x kg. Instead of D, if person E joins the room, the average weight of the persons in the room increases by 2x kg. If the weight of E is 12 kg more than that of D, then the value of x is
A bag has ₹ 785 in the denomination of ₹ 2, ₹ 5 and ₹ 10 coins. The coins are in the ratio of 6 : 9 : 10. How many coins of ₹ 5 are in the bag?
An alloy of gold and silver is taken in the ratio of 1 : 2, and another alloy of the same metals is taken in the ratio of 2 : 3. How many parts of the two alloys must be taken to obtain a new alloy consisting of gold and silver that are in the ratio 3 : 5?
In a company, 20% of the employees work in the manufacturing department. If the total salary obtained by all the manufacturing employees is one-sixth of the total salary obtained by all the employees in the company, then the ratio of the average salary obtained by the manufacturing employees to the average salary obtained by the nonmanufacturing employees is
|
218 videos|139 docs|151 tests
|