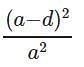Test: Probability- 1 - CAT MCQ
10 Questions MCQ Test Quantitative Aptitude (Quant) - Test: Probability- 1
A die is rolled twice. What is the probability of getting a sum equal to 9?
Hunar wrote two sections of CAT paper; Verbal and QA in the same order. The probability of her passing both sections is 0.6. The probability of her passing the verbal section is 0.8. What is the probability of her passing the QA section given that she has passed the Verbal section?
A randomly selected year is containing 53 Mondays then probability that it is a leap year
Three coins are tossed. What is the probability of getting at most two tails?
A bag contains 4 black, 5 yellow and 6 green balls. Three balls are drawn at random from the bag. What is the probability that all of them are yellow?
A bag contains 2 yellow, 3 green and 2 blue balls. Two balls are drawn at random. What is the probability that none of the balls drawn is blue?
There are 15 boys and 10 girls in a class. If three students are selected at random, what is the probability that 1 girl and 2 boys are selected?
A coin of diameter 'd' is tossed which lands on a square tile of side 'a'. What is the probability that the coin will fall completely within the tile
In a plane, S lines of lengths 2, 3, 4, 5 and 6 cm are lying. What is the probability that by joining the three randomly chosen lines end to end a triangle cannot be formed?
There are 7 boys and 8 girls in a class. A teacher has 3 items viz a pen, a pencil and an eraser, each 5 in number. He distributes the items, one to each student. What is the probability that a boy selected at random has either a pencil or an eraser?
|
191 videos|133 docs|110 tests
|