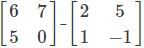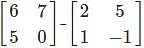Mathematics: CUET Mock Test - 1 - CUET MCQ
30 Questions MCQ Test CUET Mock Test Series - Mathematics: CUET Mock Test - 1
Match List I with List II

Choose the correct answer from the options given below:

Consider the following statements:
1. The relation f defined by 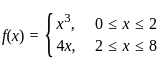 is a function.
is a function.
2. The relation g defined by 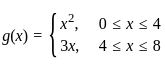 is a function.
is a function.
Which of the statements given above is/are correct?
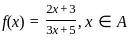 If f is to be onto, then what are A and B equal to ?
If f is to be onto, then what are A and B equal to ?
The value of log32 ⋅ log43 ⋅ log54 ⋅ log65 ⋅ log76 ⋅ log87 is-
Let a binary operation ‘*’ be defined on a set A. The operation will be commutative if ________
Which of the following relations is symmetric but neither reflexive nor transitive for a set A = {1, 2, 3}.
If f : R→R, g(x) = 3 x 2 + 7 and f(x) = √x, then gοf(x) is equal to _______
Let I be a set of all lines in a XY plane and R be a relation in I defined as R = {(I1, I2):I1 is parallel to I2}. What is the type of given relation?
If f : R → R is given by f(x) = (5 + x4)1/4, then fοf(x) is _______
Let ‘*’ be a binary operation on N defined by a * b =a - b + ab2, then find 4 * 5.
[-1, 1] is the domain for which of the following inverse trigonometric functions?
Let M={7,8,9}. Determine which of the following functions is invertible for f:M→M.
Let R be a relation in the set N given by R={(a,b): a+b=5, b>1}. Which of the following will satisfy the given relation?
If f: N→N, g: N→N and h: N→R is defined f(x) = 3x - 5, g(y) = 6y2 and h(z) = tanz, find ho(gof).
Let ‘*’ be defined on the set N. Which of the following are both commutative and associative?
Let ‘*’ be a binary operation defined by a * b = 4ab. Find (a * b) * a.
|
8 docs|148 tests
|



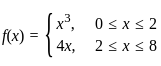 is a function.
is a function.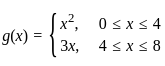 is a function.
is a function.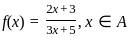
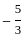
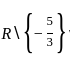
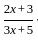
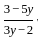
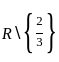
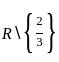
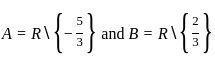
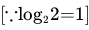

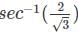 .
.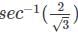 = y
= y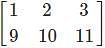 and B =
and B =  , then find A + B.
, then find A + B.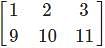 and B =
and B =
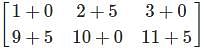
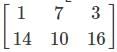
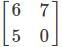 and A =
and A = 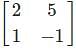 . Find the matrix B.
. Find the matrix B.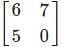 and A =
and A =