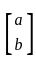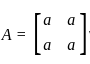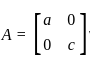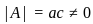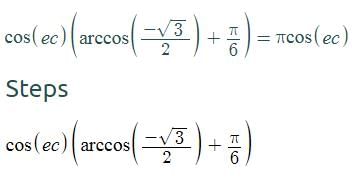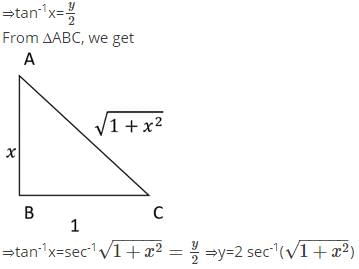Mathematics: CUET Mock Test - 4 - CUET MCQ
30 Questions MCQ Test CUET UG Mock Test Series 2026 - Mathematics: CUET Mock Test - 4
Let A be any m×n matrix, then A2 can be found only when
Let the probability density function of a random variable x be given as
f(x) = ae-2|x|
The value of ‘a’ is __________.
If X is a random variable with Mean μ, then the variance of X, denoted by Var (X) is given by:
Simplex method of solving linear programming problem uses
Find the general solution of the differential equation 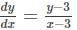 (x, y≠3).
(x, y≠3).
Which of the following functions is a solution for the differential equation xy’ - y = 0?
Which of the following differential equations given below has the solution y = logx?
Which of the following functions is a solution for the differential equation dy/dx -14x = 0?
Match List-I with List-II:
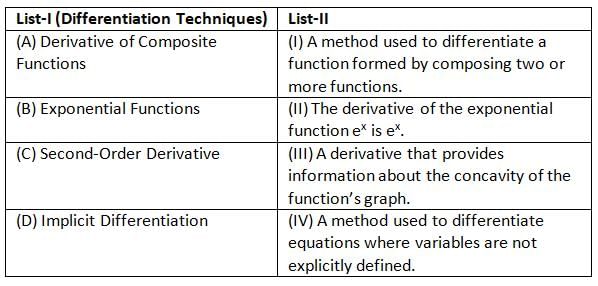
Choose the correct answer from the options given below:
Match List-I with List-II:
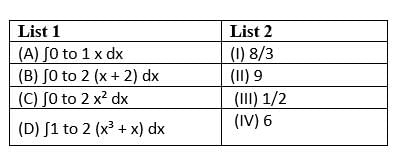
Choose the correct answer from the options given below:
Which of the following functions is the solution of the differential equation dy/dx + 2y = 0?
Which one of the following is correct if we differentiate the equation xy = aex + be-x two times?
Let A be a 2 × 2 symmetric matrix with integer entries. Then A is invertible if
1. the first column of A is the transpose of the second row of A
2. the second row of A is the transpose of first column of A
3. A is a diagonal matrix with nonzero entries in the main diagonal
If, A normal is drawn at a point P(x, y) of a curve. It meets the x-axis at Q. If PQ is of constant length k. What kind of curve is passing through (0, k)?
What is the solution of the given equation (D + 1)2y = 0 given y = 2 loge 2 when x = loge 2 and y = (4/3) loge3 when x = loge3?
What is the differential equation of all parabolas whose directrices are parallel to the x-axis?
Which of the following is the valid differential equation x = a cos(αt + β)?
A curve passes through (1, 1) such that the triangle formed by the coordinate axes and the tangent at any point of the curve is in the first quadrant and has its area equal to 2. What will be the equation of the curve?
What is the solution of dy/dx = (6x + 9y – 7)/(2x + 3y – 6)?
What will be the general solution of the differential equation d2y/dx2 = e2x(12 cos3x – 5 sin3x)? (here, A and B are integration constant)
What is the differential equation whose solution represents the family y = ae3x + bex?
A curve passes through (1, 1) such that the triangle formed by the coordinate axes and the tangent at any point of the curve is in the first quadrant and has its area equal to 2. What is the differential equation?
If y = t(x) be a differentiable function ∀ x ∈ ℝ, then which of the following is always true?
|
39 docs|145 tests
|


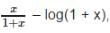 where x>0, then f is
where x>0, then f is 
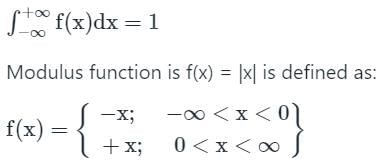
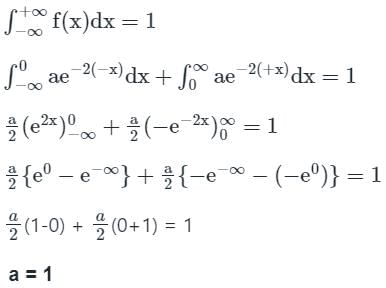
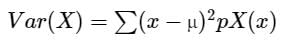
 ?
? is 2. Therefore, the order of the matrix is 2×2(m×n)
is 2. Therefore, the order of the matrix is 2×2(m×n)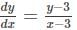
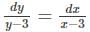
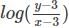 = logC1
= logC1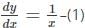
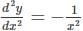
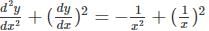
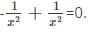
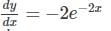
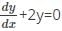
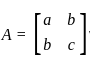
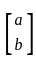 and
and 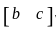 are transpose
are transpose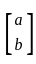 =
= 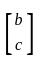
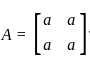
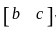 and
and 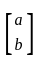 and are transpose
and are transpose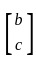 =
=