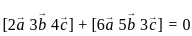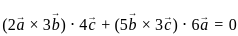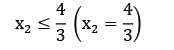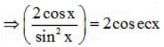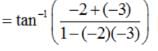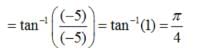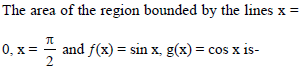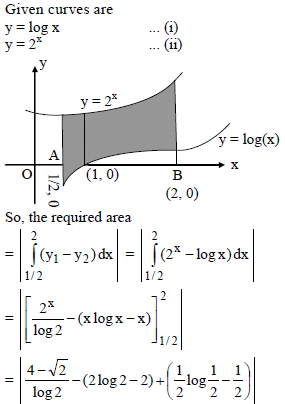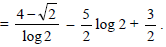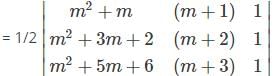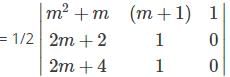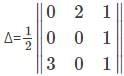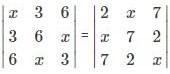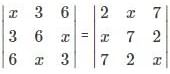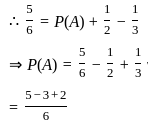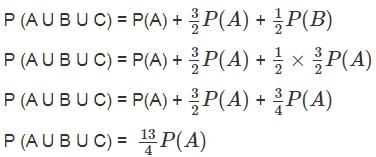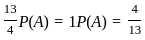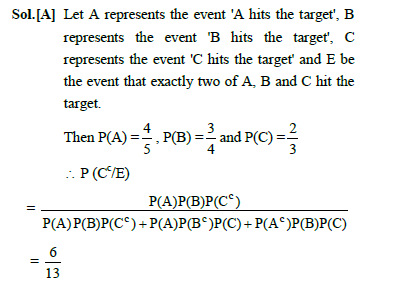Mathematics: CUET Mock Test - 7 - CUET MCQ
30 Questions MCQ Test CUET UG Mock Test Series 2026 - Mathematics: CUET Mock Test - 7
If Rs. x is the monthly increase in subscription amount, then the number of subscribers are
The number of subscribers which gives the maximum revenue is
The general solution of the differential equation ydx − xdy = 0 is
A random variable has the following probability distribution

The value of is P(X<3) is
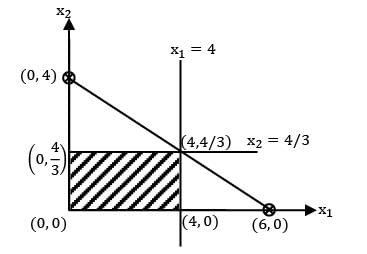
For a given LPP, Z = 50x1 + 25x2 (max) s/t: 2x1 + 3x2 ≤ 12
![]()
![]()
x1 , x2 ≥ 0
The type of solution obtained is
Find the area bounded by x = 1/2, x = 2, y = loge x and y = 2x -
Min z = 4x1 + 6x2
s/t: x1 + x2 ≤ 4
x1 + 2x2 ≥ 6
x1, x2 ≥ 0
The type of solution is
Which of the following type of solution is not possible in simplex method?
Which of the following statements are true?
I. Simplex method can handle only ≤ type constraints
II. Simplex method can be applied only when the number of decision variables are ≥ 3
III. Simplex method can be applied to only maximization problems
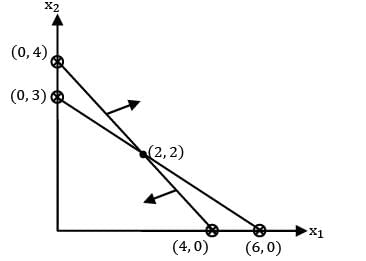
The co-ordinates of the vertices of a triangle are [m(m + 1), (m + 1)], [(m + 1)(m + 2), (m + 2)] and [(m + 2)(m + 3), (m + 3)]. Then which one among the following is correct?
What is the area of the triangle if the vertices are (0,2), (0, 0), (3, 0)?
Match List-I with List-II:
Choose the correct answer from the options given below:
Match List-I with List-II:

Choose the correct answer from the options given below:
Find the minor and cofactor respectively for the element 3 in the determinant Δ=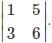
Given a matrix A= 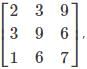 which of the elements aij follows the condition i=j.
which of the elements aij follows the condition i=j.
If A and B are two events such that P(A⋃B) = 5/6, P(A⋂B) = 1/3, P(B) = ½, then the events A and B are
If A, B, C are three mutually exclusive and exhaustive events such that if P(B) = 3/2 P(A) and P(C) = 1/2 P(B), then P(A) = _______
Match List-I with List-II:
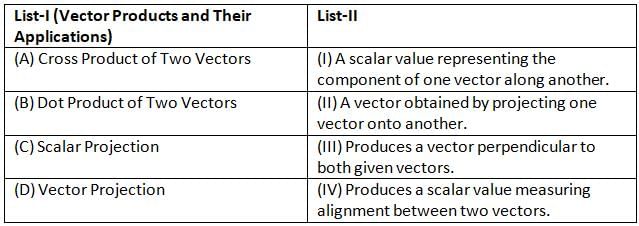
Choose the correct answer from the options given below:
A can hit a target 4 times in 5 shots, B three times in 4 shots and C twice in 3 shots. They fire a target if exactly two of them hit the target then the chance that it is C who has missed is
The slope of the tangent to the curve x = a sin t, y = a at the point ‘t’ is
|
39 docs|145 tests
|



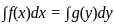
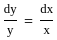
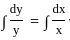
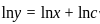

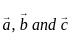 are coplanar, then what is
are coplanar, then what is  equal to?
equal to?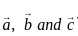 are coplanar if and only if [a b c] = 0
are coplanar if and only if [a b c] = 0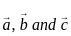 are coplanar i.e
are coplanar i.e 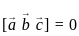
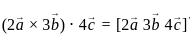 and
and 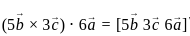
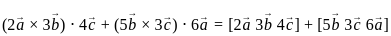
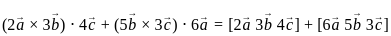
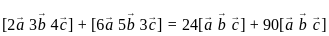
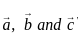 are coplanar if and only if [a b c] = 0
are coplanar if and only if [a b c] = 0