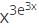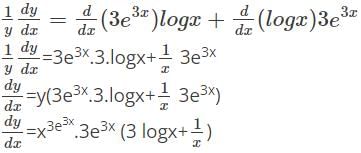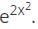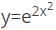Mathematics: CUET Mock Test - 10 - CUET MCQ
30 Questions MCQ Test CUET UG Mock Test Series 2026 - Mathematics: CUET Mock Test - 10
Assertion (A): The probability of success remains constant across trials in a binomial distribution.
Reason (R): The outcome of each trial is dependent on the outcome of the previous trials.
Find the values of x and y for the given system of equations.
3x-2y=3
2x+2y=4
3x-2y=3
2x+2y=4
The solution of the differential equation xdy − ydx = 0 represent family of
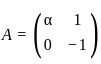 and
and 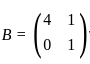 , such that A2 = B, then the value of α is:
, such that A2 = B, then the value of α is:
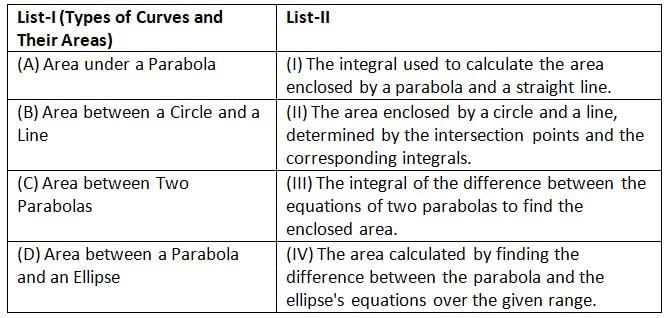
Match List-I with List-II:
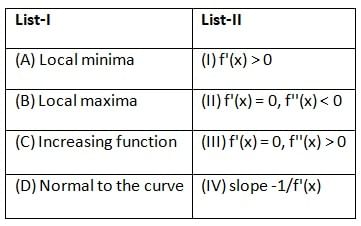
Choose the correct answer from the options given below:
Let f(x) = x4 − 2x2 + 5 be defined on [−2, 2]
Statement-1: The range of f(x) is [2,13]
Statement-2: The greatest value of f is attained at x = 2
The complete solution set of the inequality cos−1(cos4) > 3x2 − 4x is
are any three vectors then the correct expression for distributivity of scalar product over addition is
If l, m, n are the direction cosines and a, b, c are the direction ratios of a line then
The perpendicular bisector of a line segment with end points (1,2,6) and (−3,6,2) passes through (−6,2,4) and has the equation of the form 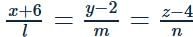 (Where l,m,n are integers, l is a prime number and l>0), then the value of lmn−(l+m+n) equals to
(Where l,m,n are integers, l is a prime number and l>0), then the value of lmn−(l+m+n) equals to
A doctor is to visit a patient. From the past experience, it is known that the probabilities that he will come by train, bus, and scooter or by other means of transport are respectively 0.3, 0.2, 0.1 and 0.4. The probabilities that he will be late are 1/4 , 1/3 and 1/12, if he comes by train, bus and scooter respectively, but if he comes by other means of transport, then he will not be late. When he arrives, he is late. The probability that he comes by bus is:
If P(A) = 5/13, P(B) = 7/13 and P(A∩B) = 3/13, evaluate P(A|B).
The length of the rectangle is changing at a rate of 4 cm/s and the area is changing at the rate of 8 cm/s. What will be the rate of change of width if the length is 4cm and the width is 1 cm.
Find the second order derivative of y=3x2 1 + log(4x)
For which of the values of x, the rate of increase of the function y=3x2-2x+7 is 4 times the rate of increase of x?
What is the slope of the tangent to the curve y = 2x/(x2 + 1) at (0, 0)?
What will be the differential function of √(x2 + 2)?
Match List-I with List-II:
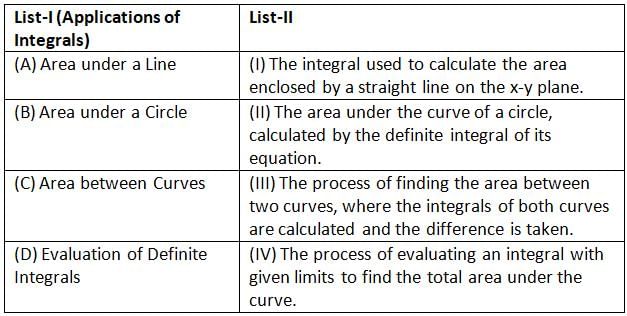
Choose the correct answer from the options given below:
Match List-I with List-II:
Choose the correct answer from the options given below:
|
39 docs|145 tests
|


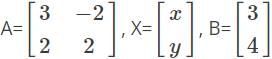
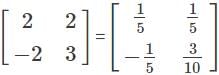
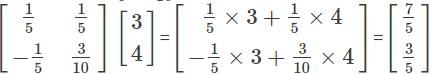

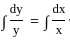
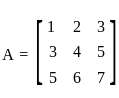 and
and 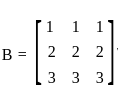 , then det(A + B) = ?
, then det(A + B) = ?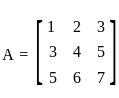 and
and 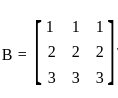
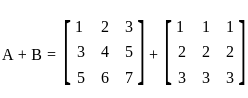
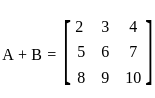
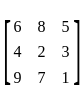 is,
is,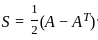 and K is the symmetric part which is given as
and K is the symmetric part which is given as 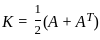 .
.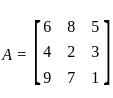
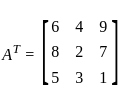

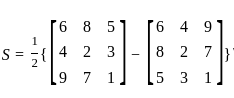
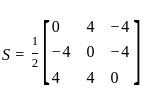
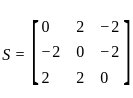
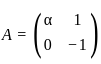 and
and 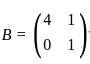 such that A
such that A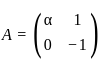 and
and 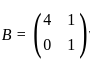
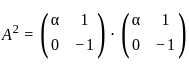
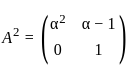
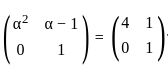

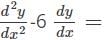 48x2−96x3−12
48x2−96x3−12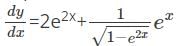
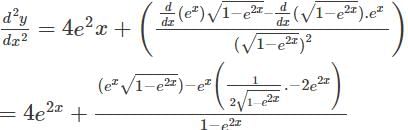
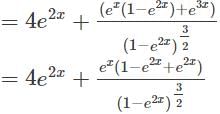

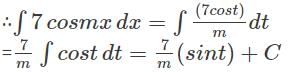
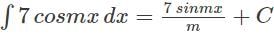
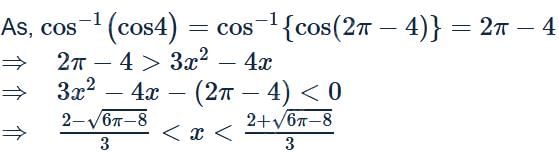
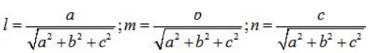

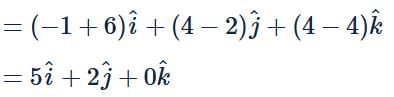
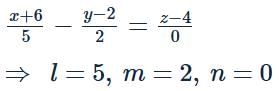
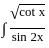 dx =
dx =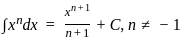
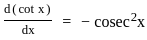
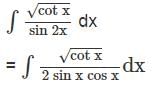
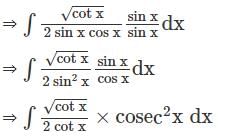
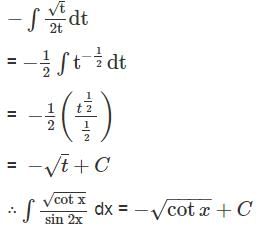
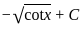 .
.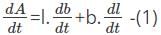
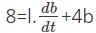
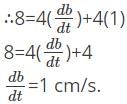
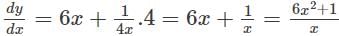
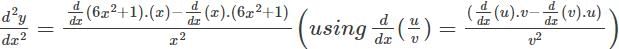
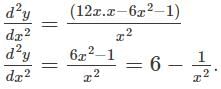
 logx w.r.t x.
logx w.r.t x.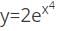 logx
logx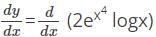
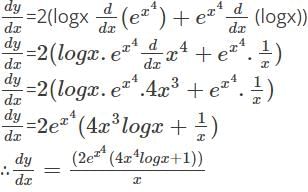
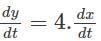
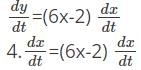
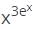 with respect to x.
with respect to x.