Mathematics: CUET Mock Test - 2 - CUET MCQ
30 Questions MCQ Test - Mathematics: CUET Mock Test - 2
Find the general solution of the differential equation 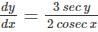 .
.
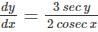 .
.Find the general solution of the differential equation 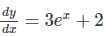
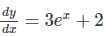
Find the particular solution of the differential equation 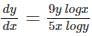 .
.
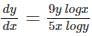 .
.The area of the smaller segment cut off from the circle x2+y2 = 9by x = 1 is
Find the unit vector in the direction of vector where P and Q are the points (1, 2, 3) and (4, 5, 6), respectively
The distance of a point whose position vector is from the plane
A particle moves in a horizontal straight line under retardation kv3, where v is the velocity at time t and k is a positive constant. If initial velocity be u and x be the displacement at time,then which one is correct?
The distance s of a particle moving along a straight line from a fixed-pointO on the line at time t seconds after start is given by x = (t – 1)2(t – 2)2. What will be the distance of the particle from O when its velocity is zero?
A pipe can empty (5/6)th part of a cistern in 20 minutes. The part of cistern which will be empty in 9 minutes is:
The system of linear inequalities 2x − 1 ≥ 3 and x − 3 > 5 has solution:
The values of x which statisfied |3x| ≥ |6 − 3x|
A. (0, 1]
B. [1, 4]
C. (4, ∞)
D. (−1, 0)
E. (−∞, 0)
Choose the correct answer from the options given below:
If  is skew symmetric matrix, then value of x2 + y2 + z2 + u2 + v2 + w2 is:
is skew symmetric matrix, then value of x2 + y2 + z2 + u2 + v2 + w2 is:
Let A = 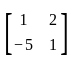 and A-1 = xA + yI, then value of x and y are
and A-1 = xA + yI, then value of x and y are
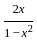 ) with respect to sin-1(
) with respect to sin-1(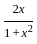 ) is equal to
) is equal to
Find the particular solution of the differential equation 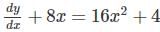 given that y = 1/3 when x = 1.
given that y = 1/3 when x = 1.
The area bounded by the curve y2 = x,line y = 4 and y – axis is equal to


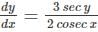
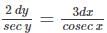
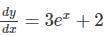
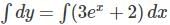 -----(1)
-----(1)
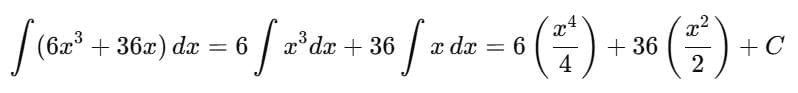
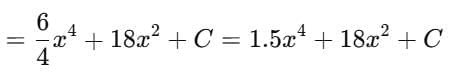
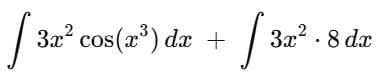
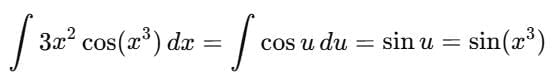
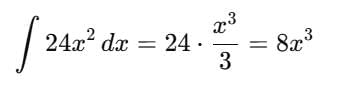
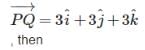
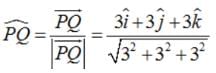
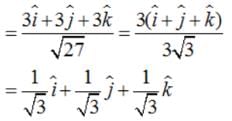
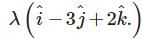
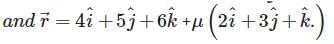

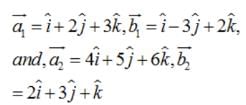
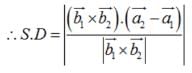
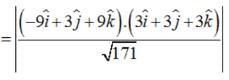
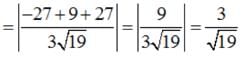
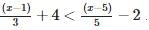
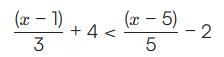
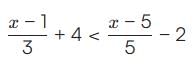
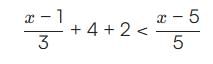

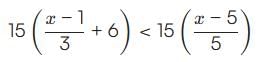
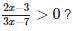
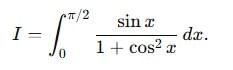

 .... (1)
.... (1)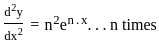
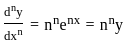
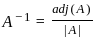 where adj(A) is called an adjoint matrix.
where adj(A) is called an adjoint matrix.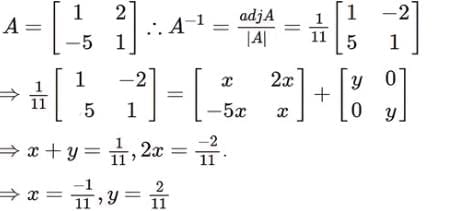
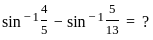
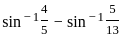

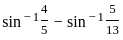
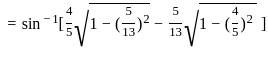
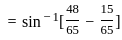
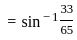
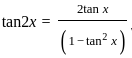
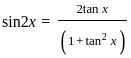
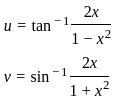
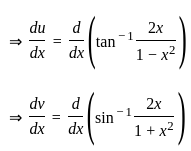

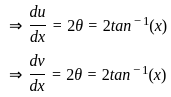
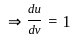
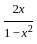
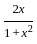
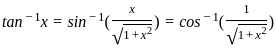
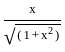 )
)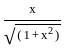 , since sin(sin
, since sin(sin











