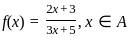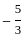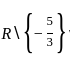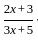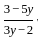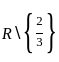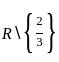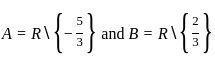Mathematics: CUET Mock Test - 1 - CUET MCQ
30 Questions MCQ Test - Mathematics: CUET Mock Test - 1
If the probability of solving a problem by three students are 1/2,1/3 and 1/4 then probability that the problem will be solved-
Five horses are in a race. Mr. A selects two of the horses at random and bets on them. The probability that Mr. A selected the winning horse is-
Three houses are available in a locality. Three persons apply for the houses. Each applies for one house without consulting others. The probability that all the three apply for the same house is
Three numbers are chosen at random without replacement from {1, 2, 3, ....8}. The probability that their minimum is 3, given that their maximum is 6, is :
The angle θ between the planes A1x + B1y + C1z + D1 = 0 and A2 x + B2 y + C2 z + D2 = 0 is given by
Find the equation of the plane through the line of intersection of the planes x + y + z = 1 and 2x + 3y + 4z = 5 which is perpendicular to the plane x – y + z = 0.
By solving the inequality 3(a - 6) < 4 + a, the answer will be
If 3x + 22x ≥ 5x, then the solution set for x is:
The equation of the tangent to the curve y = e2x at the point (0, 1) is
A particle moves with uniform acceleration along a straight line and describes distances 21m, 43m and 91m at times 2, 4 and 7 seconds,respectively.What is the distance described by the particle in 3 seconds?
The number of all possible matrices of order 3×3 with each entry 0 or 1 is
Match List I with List II

Here a = b(mod c) means b is the remainder we get when a is divided by c
List II contains the remainders.
Choose the correct answer from the options given below:
Let A be any m×n matrix, then A2 can be found only when
Consider the following statements:
1. The relation f defined by 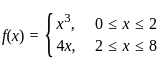 is a function.
is a function.
2. The relation g defined by 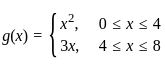 is a function.
is a function.
Which of the statements given above is/are correct?
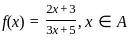 If f is to be onto, then what are A and B equal to ?
If f is to be onto, then what are A and B equal to ?
The value of log32 ⋅ log43 ⋅ log54 ⋅ log65 ⋅ log76 ⋅ log87 is-
In a binomial distribution, if the probability of at least one success is greater than or equal to 9/10, then n is greater than :




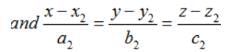
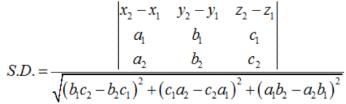

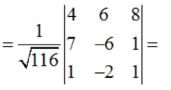
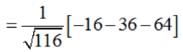
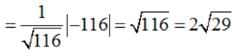

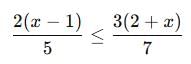
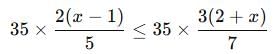


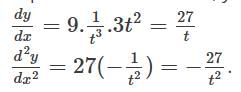
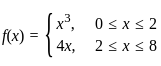 is a function.
is a function.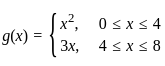 is a function.
is a function.