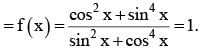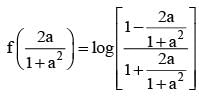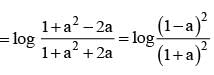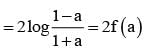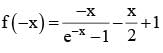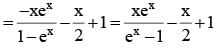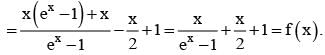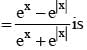JEE Advanced Level Test: Relations and Functions- 4 - JEE MCQ
30 Questions MCQ Test Chapter-wise Tests for JEE Main & Advanced - JEE Advanced Level Test: Relations and Functions- 4
The critical point of f (x) = |x- 1| is
IF f (x) = a log x + bx2 + x has extreme values at x = -1, x = 2 then a = ...., b = .....
If x is real then the minimum value of 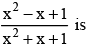
The value of “a” for which the sum of the squares of the roots of the equation x2 - (a - 2) x - a - 1 = 0 assume the least value is
A wire of length 2 units is cut into two parts which are bent respectively to form a square of side = x unit and circle of radius = r units. If the sum of the area of the square and the circle so found is minimum then
The function f (x) = 4x5 - 25x4 + 40x3 - 10 has
The function x4 - 62x2 + ax + 9 attains its maximum value at x = 1, on the interval [0, 2] then value of ‘a’ is
The longest distance of the point (a, 0) from the curve 2x2 + y2- 2x is
The point on the curve y = x2 which is nearest to (3, 0) is
The difference between the greatest and least value of the function f (x) = sin 2x - x on
The sides of a rectangle of the greatest area which can be inscribed into an ellipse
A window is in the shape of a rectangle surmounted by a semi circle. If the perimeter of the window is of fixed length „l‟ then the maximum area of the window is
The sum of the hypotenuse and a side of a right triangle is constant. If the area of the triangle is maximum then the angle between the hypotenuse and the given side is
The number of linear functions which map from [-1,1] onto [0, 2] is
If f (0) = 0, f (1) = 1, f (2) = 2 and f (x) = f (x - 2) + f (x - 3) for x = 3, 4, 5,&.., then f(9) =
If f (x) = cos [π2] x + cos [- π2] x where [x] is the step function, then
If f (x) is a polynomial fuction such that f (x) f (1/x) = f (x)+ f (1/x) and f (2) = 33 then f (x) =
If f (x) is a function such that f (x + y) = f (x) f (y) and f (3) = 125 then f (x) =
If f : [2, ∞) → B defined by f (x) = x2 - 4x + 5is a bijection, then B =
The function f : C → C defined by f (x) 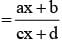 for x ∈ C where bd ≠ 0 reduces to a constant function if
for x ∈ C where bd ≠ 0 reduces to a constant function if
A function f : N → Z defined by f(n) = (n - 1)/2 when n is odd and f(n) = -n/2 when n is even, is
A = {x : |x| < 1|} and f : A → A such that f (x) = x |x|, then
The domain of the function f = {(1, 3), (3, 5), (2, 6)} is
The domain of log (x - 3) (5- x) is
The domain of log10 (x3 - x) is
|
446 docs|930 tests
|


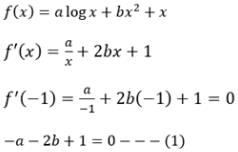
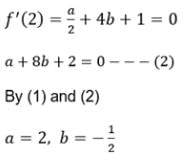

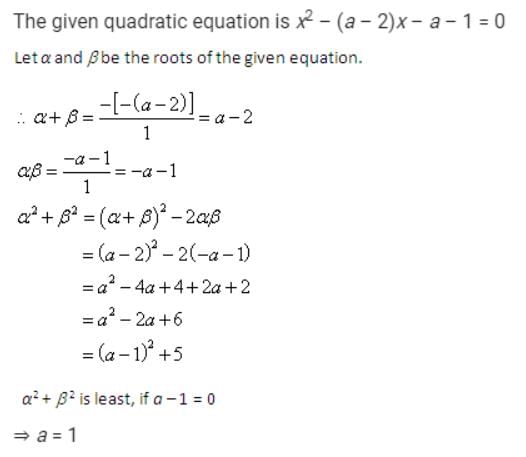
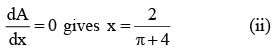
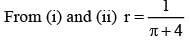
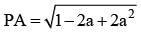
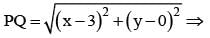
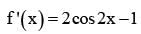
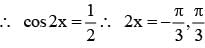
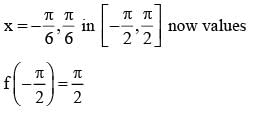
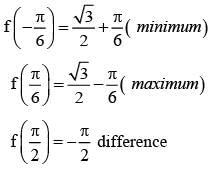
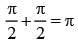
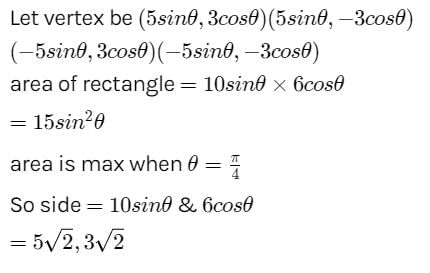
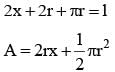
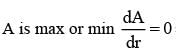
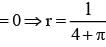
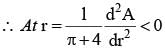
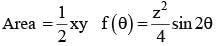
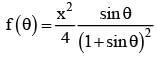
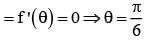
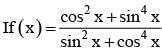 for x ∈ R Then f (2002) =
for x ∈ R Then f (2002) =