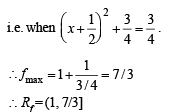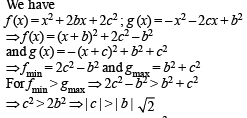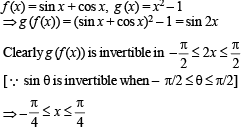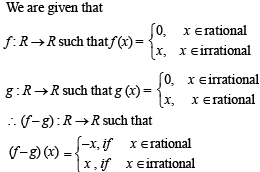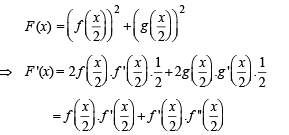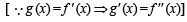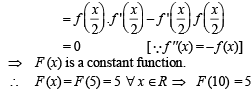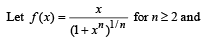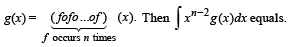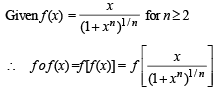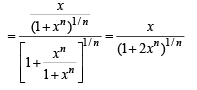JEE Advanced (Single Correct MCQs): Functions - JEE MCQ
30 Questions MCQ Test Chapter-wise Tests for JEE Main & Advanced - JEE Advanced (Single Correct MCQs): Functions
Let R be the set of real numbers. If f : R → R is a function defined by f (x) = x2, then f is :
The entire graphs of the equation y = x2 + kx – x + 9 is strictly above the x-axis if and only if
If x satisfies |x - 1| + |x - 2| + |x - 3| > 6 , then
If f ( x) = cos(ln x), then 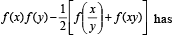 the value
the value
The domain of definition of the function
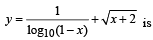
Which of the following functions is periodic?
Let f(x) = sin x and g(x) = ln | x |. If th e ran ges of th e composition functions fog and gof are R1 and R2 respectively, th en
Let f ( x) = ( x + 1)2 - 1,x > -1 . Th en th e set {x : f (x) = f -1 (x)} is
Th e fun ction f(x) = |px – q| + r | x |, x ∈ (-∞,∞) where p > 0, q > 0, r > 0 assumes its minimum value only on one point if
Let f(x) be defined for all x > 0 and be continuous. Let f(x) 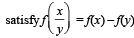 for all x, y and f(e) = 1. Then
for all x, y and f(e) = 1. Then
If the function f: [1, ∞) → [1, ∞) is defined by f(x) = 2x (x-1), then f–1 (x) is
Let f : R → R be any function. Define g : R → R by g(x) = |f(x)| for all x. Then g is
The domain of definition of the function f(x) given by the equation 2x + 2y = 2 is
Let g(x) = 1 + x - [x] and 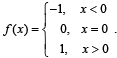 Then for allx, f(g(x)) is equal to
Then for allx, f(g(x)) is equal to
If f:[1, ∞) → [2, ∞) is given by 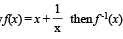 equals
equals
Let E = {1, 2, 3, 4} and F = {1, 2}. Then the number of onto functions from E to F is
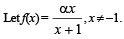 Then, for what value of a is f (f(x)) = x ?
Then, for what value of a is f (f(x)) = x ?
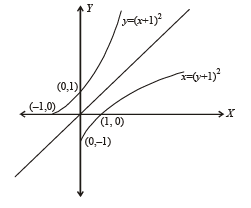
Suppose f(x) = (x + 1)2 for x > -1. If g(x) is the function whose graph is the reflection of the graph of f (x) with respect to the line y = x, then g(x) equals
Let f unction f : R → R be defined by f(x) = 2x + sin x for x ∈ R , then f is
Domain of definition of the function
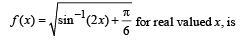
If f (x) = x2 + 2bx + 2c2 and g (x) = - x2 -2cx+ b2 such that min f (x) > max g (x), then the relation between b and c, is
If f(x) = sin x + cos x, g (x) = x2 – 1, then g (f(x)) is invertible in the domain
If the functions f(x) and g(x) are defined on R → R such that
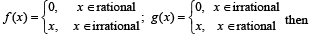
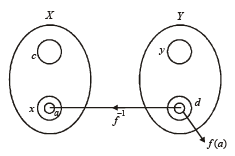
X an d Y are two sets and f : X → Y. If {f(c) = y; c ⊂ X, y ⊂ Y} and {f–1(d) = x; d ⊂ Y, x ⊂ X}, then the true statement is
If 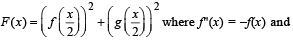 g(x) = f '(x) and given that F(5) = 5, then F(10) is equal to
g(x) = f '(x) and given that F(5) = 5, then F(10) is equal to
|
446 docs|930 tests
|


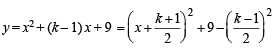
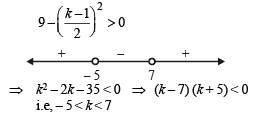

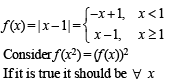
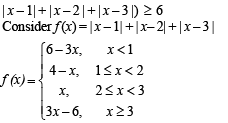
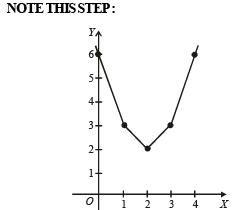
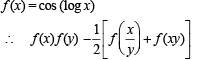
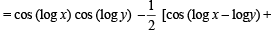
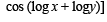
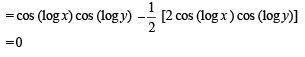
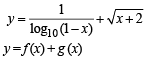
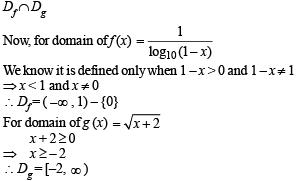
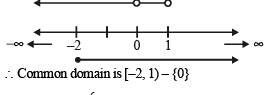
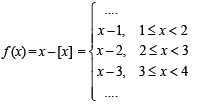
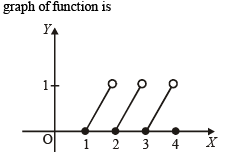
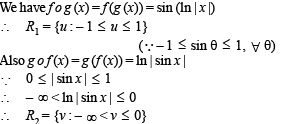
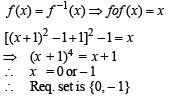
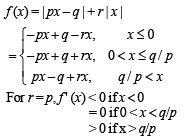
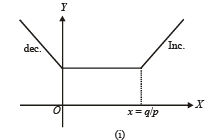
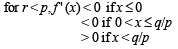
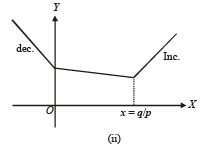
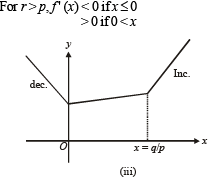
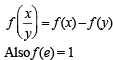
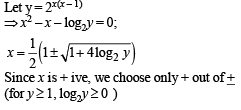
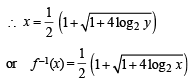

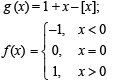
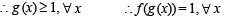
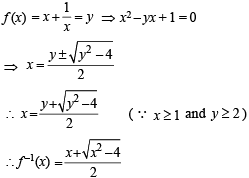
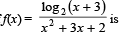
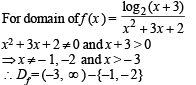
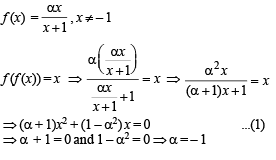
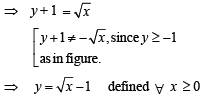
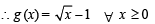

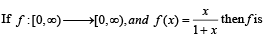
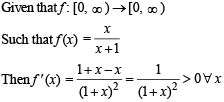

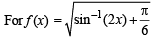 to be defined and real
to be defined and real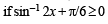
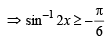 ...(1) But we know that – π/2 < sin–1 2x < π/2 ...(2) Combining (1) and (2), we get
...(1) But we know that – π/2 < sin–1 2x < π/2 ...(2) Combining (1) and (2), we get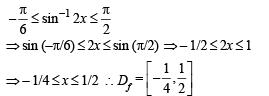
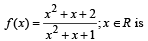
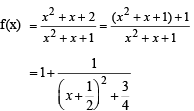
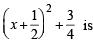 min which is so when x = – 1/2
min which is so when x = – 1/2