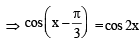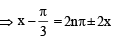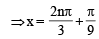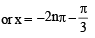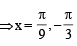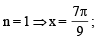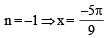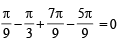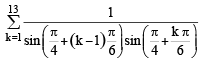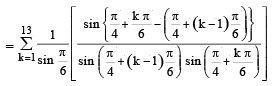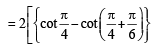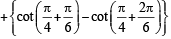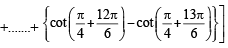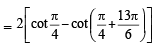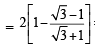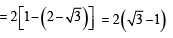JEE Advanced (Single Correct MCQs): Trigonometric Functions & Equations - NDA MCQ
29 Questions MCQ Test Mathematics for NDA - JEE Advanced (Single Correct MCQs): Trigonometric Functions & Equations
If tanθ = - 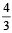 , then sinθ is (1979)
, then sinθ is (1979)
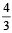 , then sinθ is (1979)
, then sinθ is (1979)If α + β + γ = 2π, then (1979)
Given A = sin2θ + cos4θ, then for all real values of θ (1980)
The equation 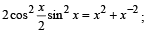
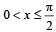 has
has
The general solution of the trigonometric equation sin x+cos x = 1 is given by : (1981 - 2 Marks)
The value of th e expression 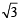 cos ec 20° – sec 20° is equal to (1988 - 2 Marks)
cos ec 20° – sec 20° is equal to (1988 - 2 Marks)
The general solution of sin x – 3 sin 2x + sin 3x = cos x – 3 cos 2x + cos 3x is (1989 - 2 Marks)
The equation (cos p – 1) x 2 + (cos p)x + sin p = 0 In the variable x, has real roots. Then p can take any value in the interval (1990 - 2 Marks)
Number of solutions of the equation tan x + sec x= 2 cosx lying in the interval [0, 2π] is : (1993)
Let 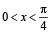 then (sec2x – tan2x) equals (1994)
then (sec2x – tan2x) equals (1994)
Let n be a positive in teger such that 
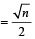 Then (1994)
Then (1994)
If ω is an imaginary cube root of unity then the value of 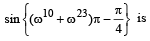 (1994)
(1994)
3 (sin x - cosx)4 + 6 (sin x + cosx)2 + 4 (sin6 x + cos6x) = (1995S)
The general values of θ satisfying the equation 2sin2θ – 3sinθ – 2 = 0 is (1995S)
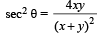 is true if and only if (1996 - 1 Mark)
is true if and only if (1996 - 1 Mark)
In a triangle PQR, ∠R =π /2 . If tan (P/2) and tan (Q/2) are the roots of the equation ax2 + bx + c = 0 (a ≠ 0) then. (1999 - 2 Marks)
Let f (θ) = sinθ(sinθ + sin3θ). Then f(θ) is (2000S)
The number of distinct real roots of 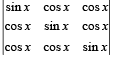 = 0 in the interval
= 0 in the interval 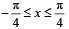 is (2001S)
is (2001S)
The maximum value of (cot α1). (cot α2 ) .... (cot αn), under the restrictions 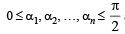 and
and 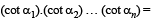 1 is (2001S)
1 is (2001S)
If α + β = π/2 and β + γ = α, then tan α equals (2001S)
The number of integral values of k for which the equation 7 cos x + 5 sin x = 2k + 1 has a solution is (2002S)
Given both θ and φ are acute an gles and 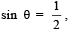
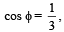 then the value of θ + φ belongs to (2004S)
then the value of θ + φ belongs to (2004S)
cos(α – β) = 1 an d cos(α + β) = 1/e where α, β ∈ [–π, π].Pairs of α, β which satisfy both the equations is/are (2005S)
The values of θ ∈ (0, 2π) for which 2 sin2θ – 5 sinθ + 2 > 0, are (2006 - 3M, –1)
Let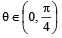 and
and 
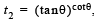
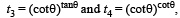 then (2006 - 3M, –1)
then (2006 - 3M, –1)
The number of solutions of the pair of equations
2sin2θ – cos2θ = 0
2cos2θ – 3sinθ = 0
in the interval [0, 2π] is (2007 - 3 Marks)
For x ∈( 0,p ) , the equation sinx + 2sin 2x – sin 3x = 3 has (JEE Adv. 2014)
Let 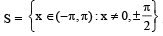 The sum of all distinct solutions of the equation
The sum of all distinct solutions of the equation
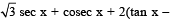 cot x) = 0 in the set S is equal to (JEE Adv. 2016)
cot x) = 0 in the set S is equal to (JEE Adv. 2016)
The value of 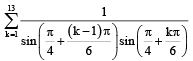 is equal to (JEE Adv. 2016)
is equal to (JEE Adv. 2016)
|
277 videos|265 docs|221 tests
|


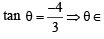 II quad or IV quad
II quad or IV quad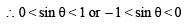
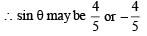
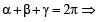
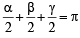
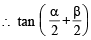
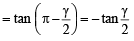
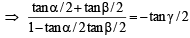

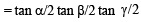

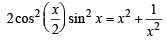 where
where 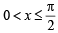

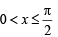
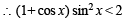
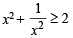
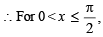
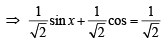
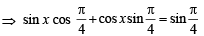

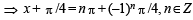 (the set of integers)
(the set of integers)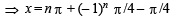
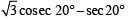
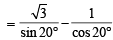
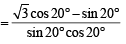
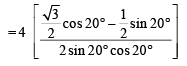
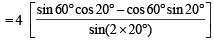
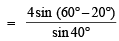

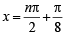
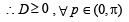
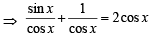
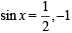

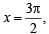 given eq. is not defined,
given eq. is not defined,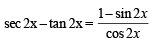
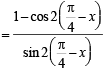
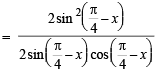
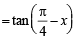
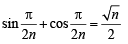
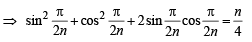
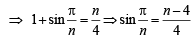
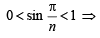
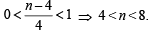
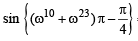
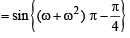
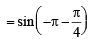
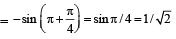
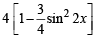
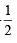 [∴ sinθ - 2=0 is not possible]
[∴ sinθ - 2=0 is not possible]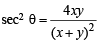

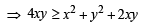
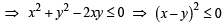
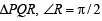

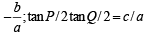
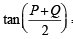
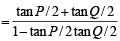
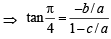
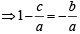
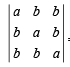 = 0 Operating C2 – C1; C3 – C2 we get
= 0 Operating C2 – C1; C3 – C2 we get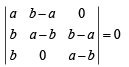
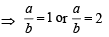
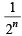 [sin 2α1 sin 2α2 .... sin2 αn ]
[sin 2α1 sin 2α2 .... sin2 αn ]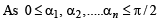
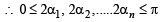
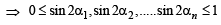
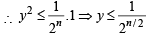
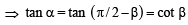
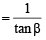
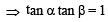
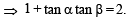
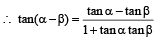
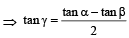
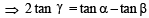
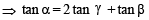
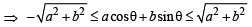
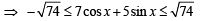
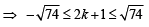
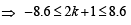
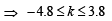
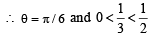
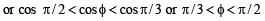
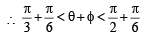
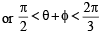
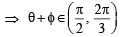
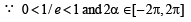
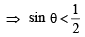
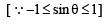
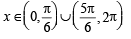
 tanθ < 1 and cotθ >1
tanθ < 1 and cotθ >1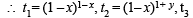
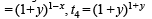

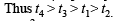
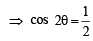
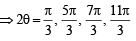
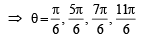 ....(1)
....(1)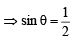
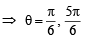 .... (2), where q ∈ [0, 2π]
.... (2), where q ∈ [0, 2π]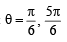
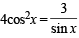
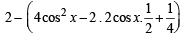
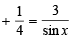

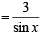
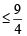 and RHS ≥ 3
and RHS ≥ 3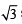 sec x + cosec x + 2 (tan x – cot x) = 0
sec x + cosec x + 2 (tan x – cot x) = 0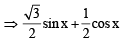 = cos2x – sin2 x
= cos2x – sin2 x