JEE Advanced Level Test: Relations and Functions- 2 - Airforce X Y / Indian Navy SSR MCQ
30 Questions MCQ Test Mathematics for Airmen Group X - JEE Advanced Level Test: Relations and Functions- 2
Let A = {1, 2, 3} and let R = {(1, 1), (2, 2), (3, 3), (1, 3), (3, 2), (1, 2)}. Then R is
Let A {a, b, c} and let R = {(a, a)(a, b), (b, a)}. Then, R is
Let A = {1, 2, 3} then total number of element in A x A is
Let S be the set of all straight lines in a plane. Let R be a relation on S defined by a R b ⇔ a ⊥ b. then, R is
Let S be the set of all real numbers and let R be a relation on S, defined by a R b ⇔ |a – b| < 1. Then, R is
Let R be the relation in the set N given by R = {(a, b): a = b – 2, b > 6}. Choose the correct answer.
Let R = {(3, 3), (6, 6), (9, 9), (3,6), (3, 9), (9, 12), (3,12), (6, 12), (12, 12)}, be a relation on the set A = {3, 6, 9, 12} Then the relation is
If f(x) = (a – xn)1/n. then f(f(x)) =
The domain of the function f = {(1, 3), (3, 5), (2, 6)} is
Let f(x) = x - 1/x +1 , x ≠ -1, then f-1 (x) is
If f(x) = x/x -1 , x ≠ 1, then f-1 (x) is
If f(x) = cos (log x), then has the value
If f(x) = x2 – 3x + 2, then (fof) (x) = ?
Let S = {1, 2, 3}. The function f : S → S defined as below have inverse for
The relation R defined on the set N of natural numbers by xRy ⇔2x2 - 3xy + y2 = 0 is
Let R = {(3, 3), (6, 6), (9, 9), (12, 12), (6, 12), (3, 9), (3, 12), (3, 6) be a relation on the set A = {3, 6, 9, 12}. The relation is
Let R be a relation on the set A of ordered pairs of positive integers defined by (x, y)R(u, v) if and only if xv = yu, then
If R be a relation defined as aRb iff |a -b|> 0, then the relation is
If R is an equivalence relation of a set A, then R-1 is
Let r be a relation from R (set of real numbers) to R defined by r = {(a, b)|a, b∈R and a - b + √3 is an irrational number}. The relation r is
|
149 videos|192 docs|197 tests
|



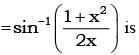
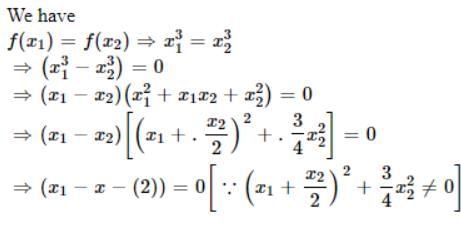
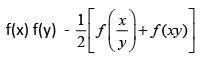
 [cos(log(x/y))+cos(log(xy))]
[cos(log(x/y))+cos(log(xy))] 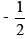 [2 cos(log x)cos(log y)] = 0
[2 cos(log x)cos(log y)] = 0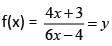
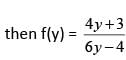
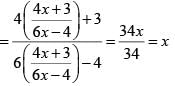

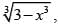 then (fof) (x) = ?
then (fof) (x) = ? 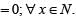
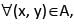
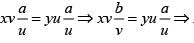 xb = ya and hence (x, y)R(a, b). Thus, R is transitive. Thus, R is an equivalent relation.
xb = ya and hence (x, y)R(a, b). Thus, R is transitive. Thus, R is an equivalent relation.