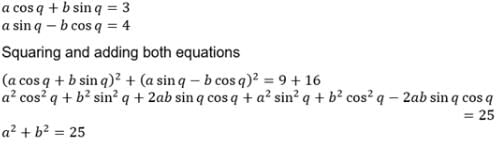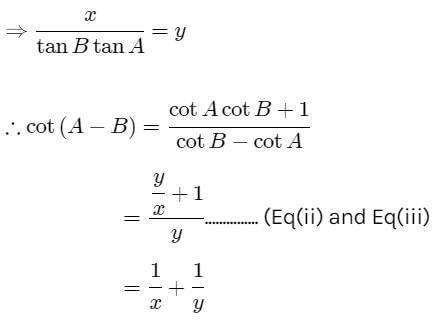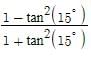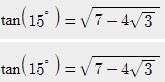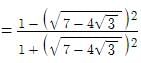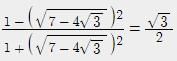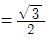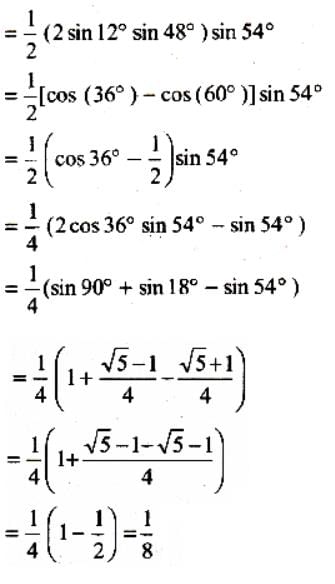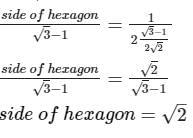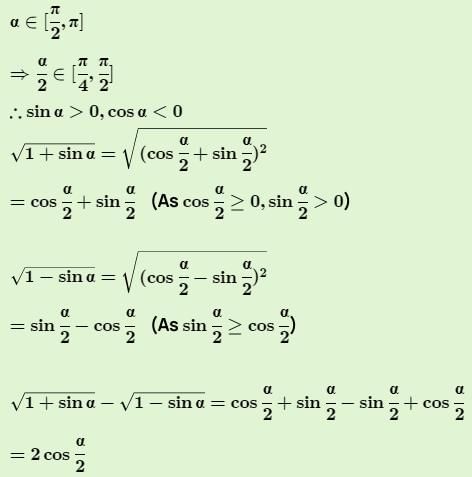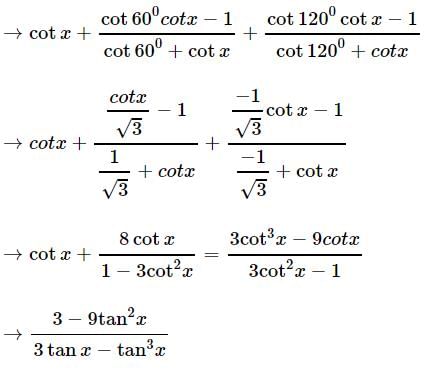JEE Advanced Level Test: Trigonometric Ratio- 1 - NDA MCQ
30 Questions MCQ Test Mathematics for NDA - JEE Advanced Level Test: Trigonometric Ratio- 1
If tan a+cot a = a then the value of tan4a+cot4a =
If a cos q + b sin q = 3 & a sin q – b cos q = 4 then a2 + b2 has the value =
The value of tan 1º tan 2º tan 3º ..... tan 89º is
cos (540º – q) – sin (630º – q) is equal to
The value of sin(p + q) sin (p - q) cosec2q is equal to
If sin a sin b – cos a cos b + 1 = 0, then the value of 1 + cot a tan b is
If 3 sina = 5 sinb, then is equal to
In a triangle ABC if tan A < 0 then :
If tan A – tan B = x and cot B – cot A = y, then cot (A – B) is equal to
If A + B = 225º, then the value of is
The value of tan 3A – tan 2A – tan A is equal to
tan 203º + tan 22º + tan 203º tan 22º =
If A lies in the third quadrant and 3 tan A – 4 = 0, then 5 sin 2A + 3 sinA + 4 cos A is equal to
If cos A = 3/4, then the value of 16cos2 (A/2) – 32 sin (A/2) sin (5A/2) is
The numerical value of sin 12º . sin 48º . sin 54º is equal to
cosθ+cos(pi/7)+cos+cos
+cos
+cos
+cos
=
A regular hexagon & a regular dodecagon are inscribed in the same circle. If the side of the dodecagon is (√3–1), then the side of the hexagon is
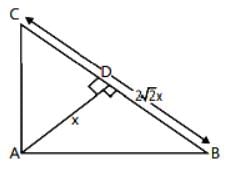
In a right angled triangle the hypotenuse is 2√2 times the perpendicular drawn from the opposite vertex. Then the other acute angles of the triangle are
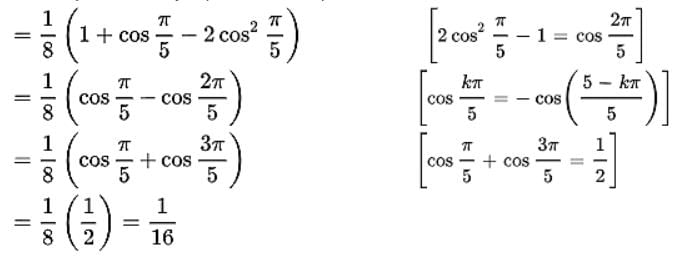
If a ∈ then the value of
–
is equal to
The value of cot x + cot(60º + x) + cot (120º + x) is equal to
If x ∈ then 4 cos2
is always equal to
|
277 videos|265 docs|221 tests
|