JEE Advanced Level Test: Vector - JEE MCQ
30 Questions MCQ Test Mathematics (Maths) Class 12 - JEE Advanced Level Test: Vector
If the vector 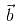 is collinear with the vector (2√2, -1,4) and
is collinear with the vector (2√2, -1,4) and 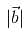 = 10, then
= 10, then
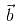 is collinear with the vector (2√2, -1,4) and
is collinear with the vector (2√2, -1,4) and 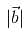 = 10, then
= 10, thenThe vertices of a triangle are A(1, 1, 2), B(4, 3, 1) and C(2, 3, 5). A vector representing the internal bisector of the angle A is
Angle between diagonals of a parallelogram whose side are represented by 
Vector 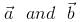 make an angle θ = 2π/3. if
make an angle θ = 2π/3. if 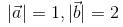 , then
, then 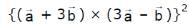 is equal to
is equal to
Unit vector perpendicular to the plane of the triangle ABC with position vectors 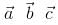 of the vertices
of the vertices
A, B, C is
If 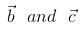 are two non-collinear vectors such that
are two non-collinear vectors such that 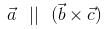 , then
, then 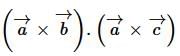 is equal to
is equal to
Vector of length 3 unit which is perpendicular to 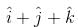 and lies in the plane of
and lies in the plane of 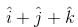 and
and 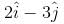
If a ,b,c are linearly independent vectors, then which one of the following set of vectors is linearly dependent ?
Let 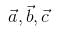 be vectors of length 3,4,5 respectively. Let
be vectors of length 3,4,5 respectively. Let 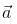 be perpendicular to
be perpendicular to 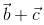 ,
,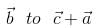 and
and 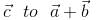 . then
. then 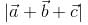
Given the vertices A (2, 3, 1), B(4, 1, –2), C(6, 3, 7) & D(–5, –4, 8) of a tetrahedron. The length of the altitude drawn from the vertex D is
for a non zero vector 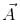 If the equations
If the equations  hold simultaneously, then
hold simultaneously, then
The volume of the parallelopiped constructed on the diagonals of the faces of the given rectangular parallelopiped is m times the volume of the given parallelopiped. Then m is equal to
If u and v are unit vectors and θ is the acute angle between them, then 2u × 3v is a unit vector for
The value of a, for which the points A,B,C with position vectors 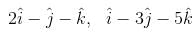 and
and 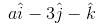 respectively are the vertices of a right angled triangle with C = π/2 are
respectively are the vertices of a right angled triangle with C = π/2 are
A particle is acted upon by constant forces 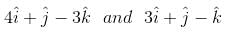 which displace ot from a point
which displace ot from a point 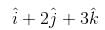 to the point
to the point 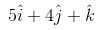 . The workdone in standard units by the force is given by
. The workdone in standard units by the force is given by
If 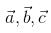 are non-coplaner vectors and λ is a real number, then the vectors
are non-coplaner vectors and λ is a real number, then the vectors 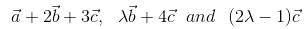 are non-coplaner for
are non-coplaner for
Let 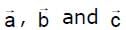 be non zero vectors such that
be non zero vectors such that 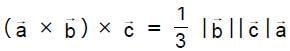 , If θ is the acute angle between the vectors
, If θ is the acute angle between the vectors  , then sin θ equals is
, then sin θ equals is
The vectors 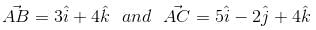 are the sides of a triangle ABC. The length of the median through A is
are the sides of a triangle ABC. The length of the median through A is
Let 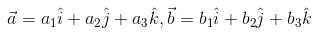 and
and 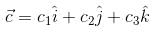 be three non-zero vectors such that
be three non-zero vectors such that 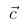 is a unit vector perpendicular to both
is a unit vector perpendicular to both 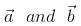 . if the angle between
. if the angle between 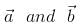 is π/6, then
is π/6, then  is equal to
is equal to
A point taken on each median of a triangle divides the median in the ratio 1 : 3, reckoning from the vertex.
Then the ratio of the area of the triangle with vertices at these points to that of the original triangle is
|
204 videos|290 docs|139 tests
|



 . The point of intersection of lines
. The point of intersection of lines 
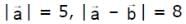 and
and 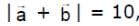 then
then 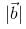 is equal to
is equal to 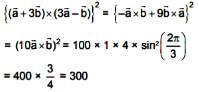
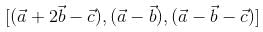 is equal to the box product
is equal to the box product 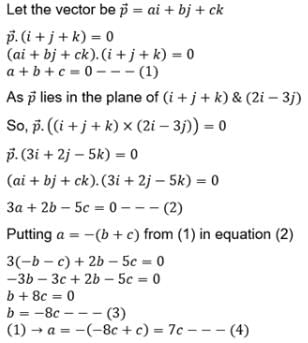
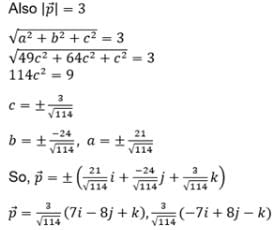
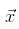 satisfying the relation
satisfying the relation 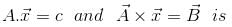
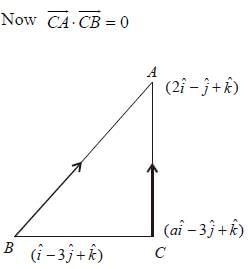
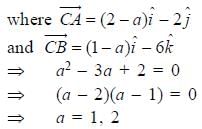
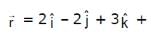
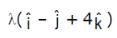 and the plane
and the plane 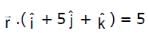 is
is 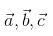 are three vectors, such that
are three vectors, such that  then
then 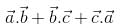 is equal to
is equal to 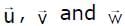 are three non-coplaner vectors, then
are three non-coplaner vectors, then 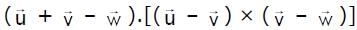 equals
equals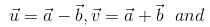
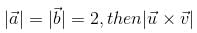 is equal to
is equal to 
















