Test: Counting Theorems - Commerce MCQ
17 Questions MCQ Test Mathematics (Maths) Class 11 - Test: Counting Theorems
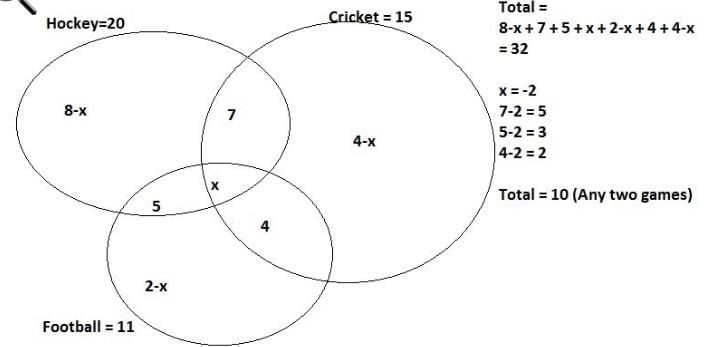
In a class of 50 students, 20 play Hockey, 15 play Cricket and 11 play Football. 7 play both Hockey and Cricket, 4 play Cricket and Football and 5 play Hockey and football. If 18 students do not play any of these given sports, how many students play exactly two of these sports?
Let A and B be two finite disjoint sets such that n(A ∪ B) = 475 and n(A) = 435, then n(B) is
If n(A) + n(B) + n(C) = n(A U B U C) then what are the sets A, B, C are called?
If in class XI of a certain school, 24 students got distinction in mathematics, 19 students got distinction in physics and 15 students got distinction in both the subjects, then the number of students in class XI is:
There is a group of 80 persons who can drive scooter or car or both. Out of these, 35 can drive scooter and 60 can drive car. Find how many can drive both scooter and car? How many can drive scooter only? How many can drive car only?(Respectively)
If P and Q are two sets such that n(P) = 120, n(Q) = 50 and n(P ∪ Q) = 140 then, n(P ∩ Q) is:
If two sets A and B are having 99 elements in common, then the number of elements common to each of the sets A × B and B × A are
If U = 100, n(A) = 30, n(B) = 40, n(A ∩ B) = 10, then n( A' ∩ B' ) =
The number of non-empty subsets of the set {1, 2, 3, 4} is
A group of 120 students, 90 take mathematics and 72 take economics. If 10 students take neither of the two, how many students take both:
In a class of 50 students, 35 students play cricket and 30 students play football; identify the students playing both the games.
In a class of 40 students 14 take physics and 29 take chemistry. If 5 students take both, how many students take neither of the subjects?
A,B,C are three sets such that n(A) = 25, n(B) = 20, n(c) = 27, n(A ∩ B) = 5, n(B ∩ C ) = 7 and A ∩ C = ∅ then n(A ∪ B ∪ C) is equal to
In a factory 70% of the workers like oranges and 64% like apples. If x% like both oranges and apples, then
|
75 videos|238 docs|91 tests
|