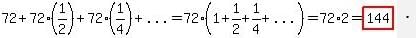Test: Progression (AP And GP)- 5 - Bank Exams MCQ
15 Questions MCQ Test IBPS Clerk Prelims 2025 Preparation - Test: Progression (AP And GP)- 5
A and B are two numbers whose AM is 25 and GM is 7. Which of the following may be a value ofA?
In a nuclear power plant a technician is allowed an interval of maximum 100 minutes. A timerwith a bell rings at specific intervals of time such that the minutes when the timer rings are notdivisible by 2, 3, 5 and 7. The last alarm rings with a buzzer to give time for decontamination ofthe technician. How many times will the bell ring within these 100 minutes and what is the valueof the last minute when the bell rings for the last time in a 100 minute shift?
The internal angles of a plane polygon are in AP. The smallest angle is 100o and the commondifference is 10o. Find the number of sides of the polygon.
Each of the series 13 + 15 + 17+…. and 14 + 17 + 20+… is continued to 100 terms. Find howmany terms are identical between the two series.
A student takes a test consisting of 100 questions with differential marking is told that eachquestion after the first is worth 4 marks more than the preceding question. If the third question ofthe test is worth 9 marks. What is the maximum score that the student can obtain by attempting 98questions?
An equilateral triangle is drawn by joining the midpoints of the sides of another equilateraltriangle. A third equilateral triangle is drawn inside the second one joining the midpoints of thesides of the second equilateral triangle, and the process continues infinitely. Find the sum of theperimeters of all the equilateral triangles, if the side of the largest equilateral triangle is 24 units.
Find the 33rd term of the sequence: 3, 8, 9, 13, 15, 18, 21, 23…
A number 20 is divided into four parts that are in AP such that the product of the first and fourth is to the product of the second and third is 2 : 3. Find the largest part.
If a clock strikes once at one o’clock, twice at two o’clock and twelve times at 12 o’clock and again once at one o’clock and so on, how many times will the bell be struck in the course of 2days?
Find the sum of the integers between 1 and 200 that are multiples of 7.
Find the sum of all odd numbers lying between 100 and 200.
The first and the last terms of an AP are 107 and 253. If there are five terms in this sequence, findthe sum of sequence.
If a, b, c are in GP, then log a, log b, log c are in
The sum of an infinite GP whose common ratio is numerically less than 1 is 32 and the sum of thefirst two terms is 24. What will be the third term?
Find the second term of an AP if the sum of its first five even terms is equal to 15 and the sum of the first three terms is equal to –3.
|
296 videos|297 docs|179 tests
|