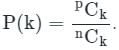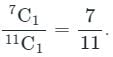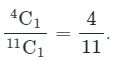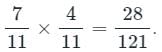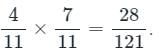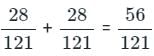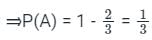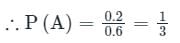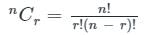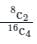Test: Probability - 3 - Grade 10 MCQ
15 Questions MCQ Test - Test: Probability - 3
If a coin is tossed thrice, find the probability of getting one or two heads.
What is the probability that a die is thrown?
(1) A even number
(2) A odd number
(3) A prime number
A bag contains 7 red and 4 blue balls. Two balls are drawn at random with replacement. The probability of getting the balls of different colors is:
Suppose P(A) = 0.4, P(B) = P and P(A ∪ B) = 0.7. If A and B are independent events, then the value of P is:
Three mangoes and three apples are in box. If two fruits are chosen at random, the probability that one is a mango and the other is an apple is
The number of possible outcomes, when a coin is tossed 6 times, is
Four dice are rolled. The number of possible outcomes in which at least one dice show 2 is
One card is drawn out of a pack of 52 cards. What is the probability that the card drawn is a heart or a king?
If 2 dice are thrown what is the probability of getting the same digits on both dice?
If P(A ∪ B) = 3/4, P(A ∩ B) = 1/4, P(A̅ ) = 2/3, then find the value of P(B).
A and B are two events such that P(B) = 0.4 and P(A ∪ B) = 0.6 If A and B are independent, then P(A) is
In a room there are eight couples. Out of them if 4 people are selected at random, the probability that they may be couples is
An unbiased coin is tossed 3 times, if the third toss gets head what is the probability of getting at least one more head?
If four dice are thrown together, then what is the probability that the sum of the numbers appearing on them is 25?
If A and B are two events such that P(A) ≠ 0 and P(B | A) = 1, then