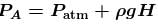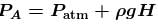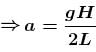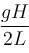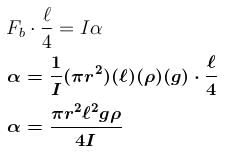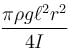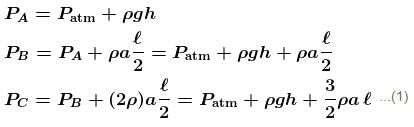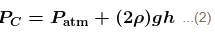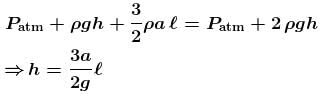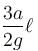Fluid Dynamics MCQ Level - 2 - Physics MCQ
10 Questions MCQ Test Topic wise Tests for IIT JAM Physics - Fluid Dynamics MCQ Level - 2
Water flows steadily from an tank as shown. Find x where the water lands. Assume area of cross-section of hole is much less than area of cross-section of tank.

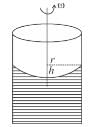
A cylindrical container of an incompressible liquid rotates with ω as shown. The density of liquid is ρ. The liquid acquires parabolic shape. Find the height of the liquid. Radius of container is r.

A shower head has 20 circular opening each of radius 1 mm. Shower head is connected to a pipe of radius 0.8 cm. The speed of water in the pipe is 3ms–1. Find the speed of water as it exists from the shower openings.
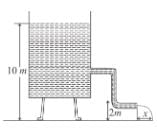
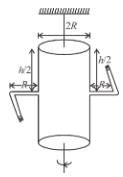
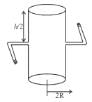
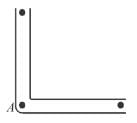
A cylindrical container of radius R and height h is completely filled with a liquid. Two horizontal L shaped pipes of small cross-section area a are connected to the cylinder as shown in the figure. Now the two pipes are opened and fluid starts coming out of the pipes horizontally in opposite directions. Then the torque due to ejected liquid on the system is :
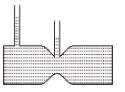
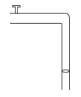
A steady stream of water falls straight down from a pipe as shown. Assume the flow is incompressible, then :
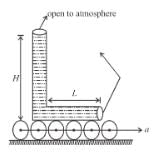
A narrow tube completely filled with a liquids lying on a series of cylinders as shown in figure. Assuming no sliding between any surfaces, the value of acceleration of the cylinders for which liquids will not come out of the tube from anywhere is given by :
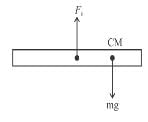
A non uniform cylinder of mass m, length l and radius r is having its centre of mass at a distance l/4 from the centre and lying on the axis of the cylinder. The cylinder is kept in a liquid of uniform density ρ. The moment of inertia of the rod about the centre of mass is I. The angular acceleration of point A relative to point B just after the rod is released from the position shown in figure is :

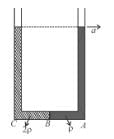
A U-tube of base length ℓ filled with same volume of two liquids of densities ρ and 2ρ is moving with an acceleration a on the horizontal plane. If the height difference between the two surfaces (open to atmosphere) becomes zero, then the height h is given by :
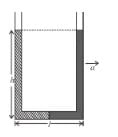
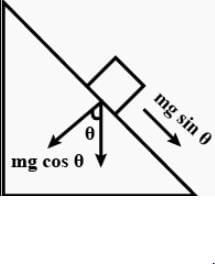
A cylindrical vessel filled with water is released on an inclined surface of angle θ as shown in figure. The friction coefficient of surface with vessel is μ (< tan θ.) Then the constant angle made by the surface of water with the incline will be :
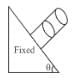
For a liquid which is following steadily, the level in the vertical tubes is best represented by :


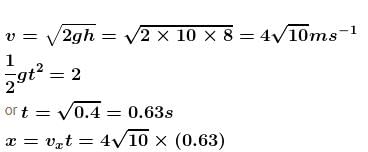
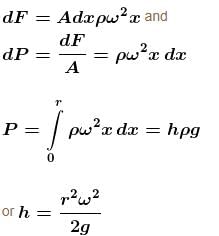
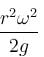

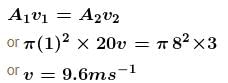
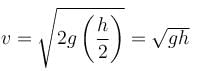
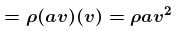
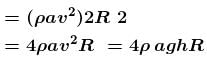

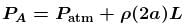 (From horizontal limb)
(From horizontal limb)