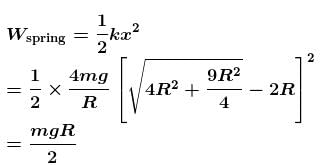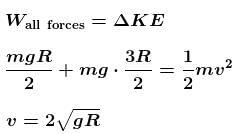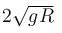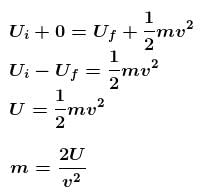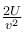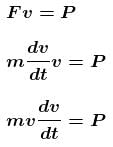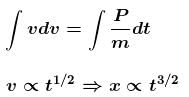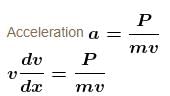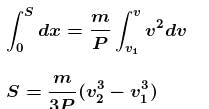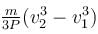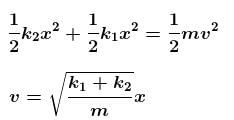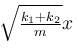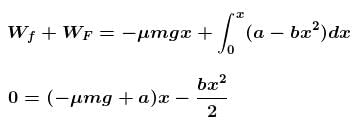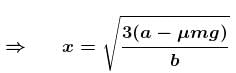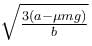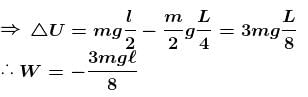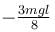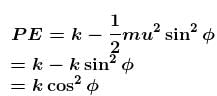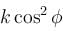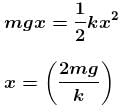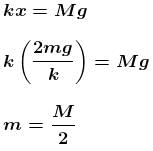Work, Power And Energy MCQ Level - 1 - Physics MCQ
10 Questions MCQ Test Topic wise Tests for IIT JAM Physics - Work, Power And Energy MCQ Level - 1
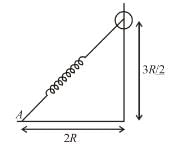
A ring of mass m can slide over a smooth vertical rod. The ring is connected to a spring of force constant k = 4mg/R where 2R is the natural length of the spring. The other end of the spring is fixed to the ground at a horizontal distance 2R from the base of the rod. The mass is released at a height of 1.5R from the ground.

A body is dropped from a certain height. When it loses U amount of its energy it acquires a velocity v. The mass of the body is :
A body is moved along a straight line by a machine delivering a constant power. The distance moved by the body in time t is proportional to :
A self propelled vehicle of mass m whose engine delivers constant power P has an acceleration a = P/mv (assume that there is no friction). In order to increase its velocity from v1 to v2 the distance it has to travel will be :
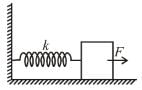
A block attached to a spring, pulled by a constant horizontal force, is kept on a smooth surface as shown in the figure. Initially, the spring is in the natural state. Then the maximum positive work that the applied force F can do is :
[Given that spring does not break]
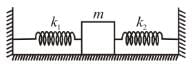
A block of mass m is attached to two unstretched springs of spring constants k1 and k2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as passes through the means position shown.
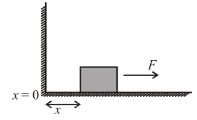
The block of mass m initially at x = 0 is acted upon by a horizontal force at any position x is given as F = a – bx2, where a > μmg, as shown in the figure. The co-efficient of friction between the surfaces of contact is μ. The net work done on the blocks is zero. If the block travels a distance?
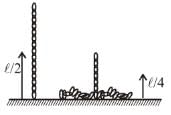
A man places a chain (of mass m and length l) on a table slowly. Initially the lower end of the chain just touches the table. The man drops the chain. When half of the chain is in vertical position. The work done by the man in this process is :
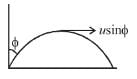
A body is projected with kinetic energy k at angle 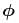 with the vertical. Neglecting friction, its potential energy at the highest point will be :
with the vertical. Neglecting friction, its potential energy at the highest point will be :
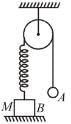
In the Figure, the ball A is released from rest when the spring is at its natural length. For the block B of mass M to leave contact with the ground of some stage, the minimum mass of A must be :