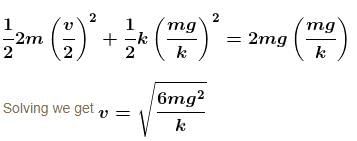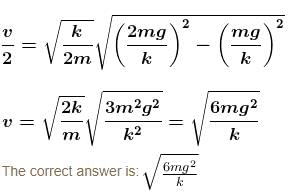Work, Power And Energy MCQ Level - 2 - Physics MCQ
10 Questions MCQ Test - Work, Power And Energy MCQ Level - 2
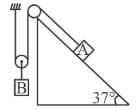
The blocks A and B shown in the figure have masses MA = 5kg and MB = 4 kg. The system is released from rest. The speed of B after A has traveled a distance 1 m along the incline is :

In the figure the variation of components of acceleration of a particle of mass 1kg is shown w.r.t. time. The initial velocity of the particle is 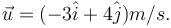 The total work done by the resultant force on the particle in time interval from t = 0 to t = 4 second is :
The total work done by the resultant force on the particle in time interval from t = 0 to t = 4 second is :
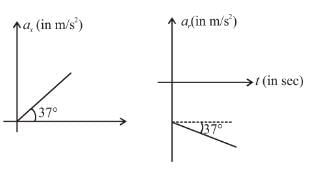
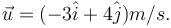 The total work done by the resultant force on the particle in time interval from t = 0 to t = 4 second is :
The total work done by the resultant force on the particle in time interval from t = 0 to t = 4 second is :
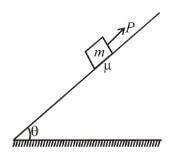
A block of mass m is being pulled up the rough incline by the agent delivering constant power P. The coefficient of friction between the block and the incline is µ. The maximum speed of the block during the courses of ascent is :

The potential energy (in SI units) of a particle of mass 2kg in a conservative fields U = 6x – 8y. If the initial velocity of the particle is 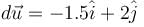 then the total distance traveled by the particle in first two seconds is :
then the total distance traveled by the particle in first two seconds is :
The potential energy of a particle of mass m free to move along x-axis is given by 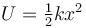 for x < 0 and U = 0 for x ≥ 0 (x denotes the x-coordinate of the particle and k is a positive constant). If the total mechanical energy of the particle is E, then its speed at x = -(2E/k)1/2
for x < 0 and U = 0 for x ≥ 0 (x denotes the x-coordinate of the particle and k is a positive constant). If the total mechanical energy of the particle is E, then its speed at x = -(2E/k)1/2
A man places a chain (of mass m and length l) on a table slowly. Initially the lower end of the chain just touches the table. The man drops the chain. When half of the chain is in vertical position, the potential energy of chain is :
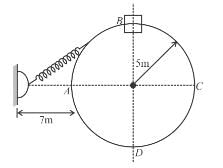
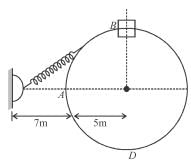
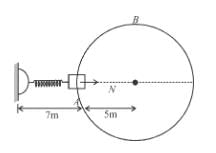
A collar B of mass 2kg is constrained to move along a horizontal smooth and fixed circular track of radius 5m. The spring lying in the plane of the circular track and having spring constant 200N/m is undeformed when the collar is at A. If the collar starts from rest at B the normal reaction exerted by the track on the collar when it passes through A is :
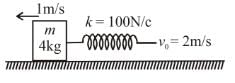
The spring block system lies on a smooth horizontal surface. The free end of the spring is being pulled towards right with constant speed v0 = 2m/s. At t = 0 sec, the spring of constant k = 100 N/cm in unstretched and the block has a speed 1m/s to left. The maximum extension of the spring is :
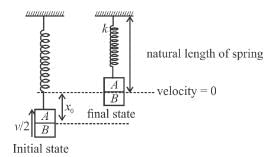
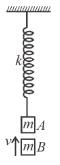
Block A is hanging from a vertical spring and is at rest. Block B strikes the block A with velocity v and sticks to it. Then the value of v for which the spring just attains natural length is :



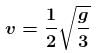
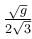
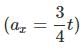 and
and 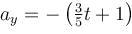
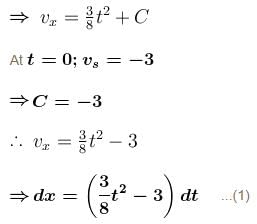
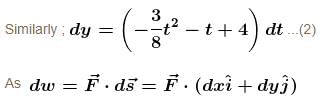
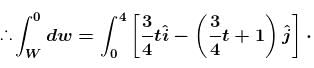


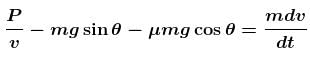
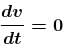
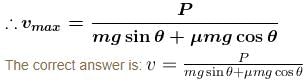
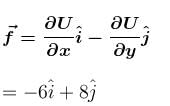
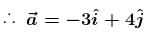 has same direction as that of
has same direction as that of 
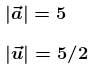
 are in same direction, particle will move along a straight line
are in same direction, particle will move along a straight line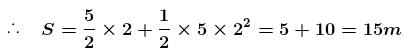
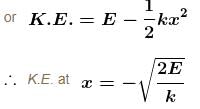
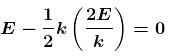
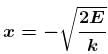 is zero.
is zero. 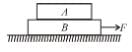
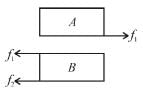
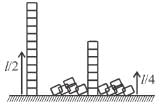
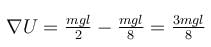
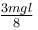
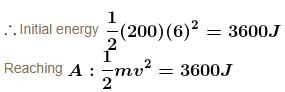
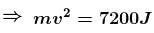
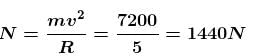
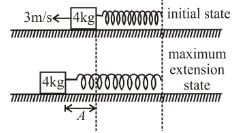

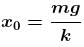
 (see fig.) and comes to rest.
(see fig.) and comes to rest.