Important Questions: Symmetry - Class 7 MCQ
20 Questions MCQ Test Mathematics (Maths) Class 7 - Important Questions: Symmetry
Which of the following alphabets has a vertical line of symmetry?
Which of the following alphabets has a horizontal line of symmetry?
Which of the following alphabets has no line of symmetry?
Which of the following alphabets has many lines of symmetry?
Which of the following triangles has no line of symmetry?
Which of the following figures are symmetrical with respect to minimum two lines?
A Which of the following figures has rotational symmetry of order more than 1?
What is the order of rotational symmetry for the given figure?

Which of the following figures has only one line of symmetry?
Identify the number of lines of symmetry for the figure given.

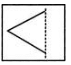
In the given figure, the dotted line is the line of symmetry. Which figure is formed if the given figure is reflected in the dotted line?
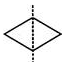
What is the other name for a line of symmetry of a circle?
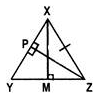
A In A XYZ, XY = XZ and XM⊥YZand ZP⊥XY. About which of the following is the triangle symmetrical?
What is the order of rotational symmetry of the English alphabet Z?
Which of these quadrilaterals have both line and rotational symmetries of order more than 3?
Which of these letters has only rotational symmetry?
A square has a rotational symmetry of order 4 about its centre. What is the angle of rotation?
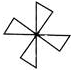
What is the order of rotational symmetry of the figure given?
|
76 videos|344 docs|39 tests
|


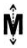

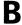 in a horizontal mirror?
in a horizontal mirror?