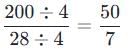Olympiad Test: Ratio & Proportion - Class 6 MCQ
20 Questions MCQ Test Mathematics (Maths) Class 6 - Olympiad Test: Ratio & Proportion
Identify the ratio of 4 seconds and 1/4 minute from the following.
A poster is 1.5 cm long and 7.5 cm wide. Which of the following is the ratio (in lowest terms) of the length and perimeter of the poster?
The length and width of a tape are 2 m and 28 cm. What is their ratio?
What is the new ratio obtained by adding 4 to the antecedent and 2 to the consequent of the ratio 3 : 8?
In a cricket coaching camp, 1200 children are trained out of which 900 are selected for various matches. What is the ratio of non-selected children to the total number of children?
What is the condition for two ratios to be equal?
What are the extremes of the proportion 9 : 3 :: 36 : 12?
What is the simplest form of the ratio 144 : 28?
If x : y : : y : z, identify the correct statement from among the following.
Fill in the blank so that the three numbers will be in proportion ___, 32, 64.
The ratios 6 : 3 and 5 : 15 are given. Which of the following is true about them?
The first, second and the third terms of a proportion are 5,120 and 40. What is the fourth term?
The first, third and the fourth terms of a proportion are 6, 12 and 36. What is the second term?
The ratio of number of boys to number of girls in a tutorial is 2 : 3. If there are 180 girls, what is the number of boys?
The ratio of lemons to number of cups of water to be mixed to prepare lemon juice is 3 : 5. For 12 lemons what is the number of cups of water required?
In a cricket team what is the ratio of total number of players to the number of wicket keepers?
In the word GEOMETRY, what is the ratio of number of consonants to the number of vowels?
|
92 videos|348 docs|54 tests
|