JEE Advanced Level Test: Continuity and Differentiability- 2 - JEE MCQ
30 Questions MCQ Test Mathematics (Maths) Class 12 - JEE Advanced Level Test: Continuity and Differentiability- 2
The function 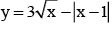 is continuous at
is continuous at
If the function 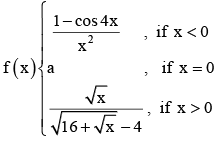 is continuous at x = 0 then a =
is continuous at x = 0 then a =
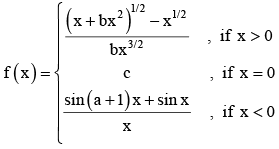 is continuous at x = 0 then
is continuous at x = 0 then
The function is discontinuous at the points
The values of a and b if f is continuous at x = 0, where
is continuous at
then k =
so that f(x) is continuous at
then
where [.] denotes greatest integer function and the function is continuous then
is continuous everywhere. Then the equation whose roots are a and b is
where [x] is the greatest integer function. The function f (x) is
The function is continuous at exactly two points then the possible values of ' a ' are
If the function is continuous for every x ∈ R then
The function f (x) = cos-1 (cos x) is
then which is correct
Let f (x) = |x - 1| + |x + 1|
The set of all points where the function is differentiable is
If then derivative of f(x) at x = 0 is
If f : R → R be a differentiable function, such that f (x + 2y) = f (x) + f (2y) + 4xy for all x, y ∈ R then
Let f be a differentiable function satisfying the condition for all
, then f ' (x) is equal to
The function is not differentiable at
then set of all points where f is differentiable is
Let h(x) = min {x, x2} for Then which of the following is correct
If f (x + y) = 2f (x) f (y) for all x, y ∈ R where f ' (0) = 3 and f (4) = 2, then f ' (4) is equal to
If and f ' (0) = -1, f (0) = 1, then f (2) =
Let f (x) be differentiable function such that and y. If
Let f : R → R be a function defined by f (x) = min {x + 1, |x| + 1}, Then which of the following is true?
|
204 videos|290 docs|139 tests
|




















