JEE Advanced Level Test: Maxima and Minima- 2 - JEE MCQ
19 Questions MCQ Test Mathematics (Maths) Class 12 - JEE Advanced Level Test: Maxima and Minima- 2
The lower corner of a leaf in a book is folded over so as to just reach the inner edge of the page. The fraction of width folded over if the area of the folded part is minimum is
If x1 and x2 are abscissa of two points on the curve f(x) = x – x2 in the interval [0, 1], then maximum value of the expression (x1 + x2) – 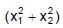 is
is
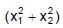 is
isLeast value of the function, f(x)=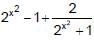 is
is
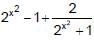 is
isA triangular park is enclosed on two sides by a fence and on the third side by a straight river bank. The two sides having fence are of same length x. The maximum area enclosed by the park is
The co-ordinate of the point for minimum value of z = 7x – 8y subject to the conditions x + y – 20 £ 0, y ³ 5, x ³ 0, y ³ 0
The equation x3 – 3x + [a] = 0, will have three real and distinct roots if
(where [*] denotes the greatest integer function)
Let f(x) = 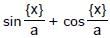 . Then the set of values of a for which f can attain its maximum values is
. Then the set of values of a for which f can attain its maximum values is
(where a>0 and { * } denotes the fractional part function)
A function is defined as f(x) = ax2 – b|x| where a and b are constants then at x = 0 we will have a maxima of f(x) if
A and B are the points (2, 0) and (0, 2) respectively. The coordinates of the point P on the line 2x+3y+1=0 are
The maximum value of f(x) = 2bx2 – x4 – 3b is g(b), where b > 0, if b varies then the minimum value of g(b) is
Number of solution(s) satisfying the equation, 3x2 – 2x3 = log2 (x2 + 1) – log2 x is
If a2x4 + b2 y4 = c6, then the maximum value of xy is
Maximum and minimum value of f(x) = max (sin t), 0 < t < x, 0 £ x £ 2p are
The function `f' is defined by f(x) = xp (1 – x)q for all x Î R, where p, q are positive integers, has a maximum value, for x equal to
The maximum slope of the curve y=–x3+3x2+2x–27 will be
Two points A(1, 4) & B(3, 0) are given on the ellipse 2x2 + y2 = 18. The co-ordinates of a point C on the ellipse such that the area of the triangle ABC is greatest is
The lateral edge of a regular hexagonal pyramid is 1 cm. If the volume is maximum, then its height must be equal to
Let f(x) = 5x – 2x2 + 2; x ∈ N then the maximum value of f(x) is
The maximum value of f(x), if f(x) + 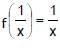 , x ∈ domain of f
, x ∈ domain of f
|
204 videos|290 docs|139 tests
|




















