JEE Advanced Level Test: Maxima and Minima - JEE MCQ
30 Questions MCQ Test Mathematics (Maths) Class 12 - JEE Advanced Level Test: Maxima and Minima
f(x) = 1 + 2x2 + 4x4 + 6x6 + ................+ 100x100 is polynomial in a real variable x, then f(x) has
On the interval [0, 1] the function x25(1 – x)75 takes its maximum value at
The product of minimum value of xx and maximum value of 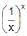 is
is
The minimum value of the function defined by f(x) = max (x, x + 1, 2 – x) is
The greatest and the least values of the function, f(x) = 2 – 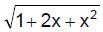 , x ∈ [–2, 1] are
, x ∈ [–2, 1] are
Let f(x) = {x}, For f(x), x = 5 is (where {*} denotes the fractional part)
The difference between the greatest and least values of the function f(x) = sin 2x – x on [–p/2, p/2] is
The radius of a right circular cylinder of greatest curved surface which can be inscribed in a given right circular cone is
The dimensions of the rectangle of maximum area that can be inscribed in the ellipse (x/4)2 + (y/3)2 = 1 are
The largest area of a rectangle which has one side on the x–axis and the two vertices on the curve y = is
The co–ordinates of the point on the curve x2 = 4y, which is at least distance from the line
y = x – 4 is
Let f(x) = 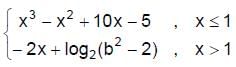 the set of values of b for which f(x) has greatest value at x = 1 is given by
the set of values of b for which f(x) has greatest value at x = 1 is given by
The set of values of p for which the extrema of the function, f(x) = x3 – 3px2 + 3(p2 – 1) x + 1 lie in the interval (–2, 4) is
Four points A, B, C, D lie in that order on the parabola y = ax2 + bx + c. The co–ordinates of A, B & D are known as A(–2, 3); B(–1, 1) and D(2, 7). The co–ordinates of C for which the area of the quadrilateral ABCD is greatest is
In a regular triangular prism the distance from the centre of one base to one of the vertices of the other base is l. The altitude of the prism for which the volume is greatest is
Two vertices of a rectangle are on the positive x–axis. The other two vertices lie on the lines y = 4x and y = –5x + 6. Then the maximum area of the rectangle is
A variable point P is chosen on the straight line x + y = 4 and tangents PA and PB are drawn from it to circle x2 + y2 = 1. Then the position of P for the smallest length of chord of contact AB is
The maximum area of the rectangle whose sides pass through the angular points of a given rectangle of sides a and b is
If p and q are positive real numbers such that p2 + q2 = 1, then the maximum value of (p + q) is
The function f(x) = 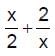 has a local minimum at
has a local minimum at
If the function f(x) = 2x3 – 9ax2 + 12a2x + 1, where a > 0, attains its maximum and minimum at p and q respectively such that p2 = q, then a equals
The maximum value x3 – 3x in the interval [0, 2] is
The minimum value of (x – p)2 + (x – q)2 + (x – r)2 will be at x equals to
The number of values of x where f(x) = cos x + cos 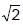 x attains its maximum value is
x attains its maximum value is
The maximum value of cos a1 . cos a2 . cos a3....cos an under the restriction 0 £ a1, a2,.....an £and cot a1 cot a2 .... cot an=1 is
|
204 videos|290 docs|139 tests
|



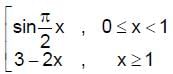 then
then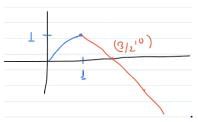
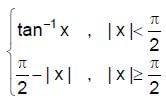 then
then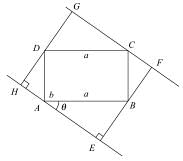
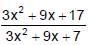 is
is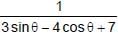 is
is
















