JEE Advanced Level Test: Monotonicity- 2 - JEE MCQ
16 Questions MCQ Test Mathematics (Maths) Class 12 - JEE Advanced Level Test: Monotonicity- 2
The values of p for which the function
f(x)=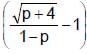 x5 – 3x + ln 5 decreases for all real x is
x5 – 3x + ln 5 decreases for all real x is
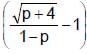 x5 – 3x + ln 5 decreases for all real x is
x5 – 3x + ln 5 decreases for all real x is For which values of `a' will the function
f(x) = x4 + ax3 + 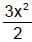 + 1 will be concave upward along the entire real line
+ 1 will be concave upward along the entire real line
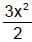 + 1 will be concave upward along the entire real line
+ 1 will be concave upward along the entire real lineThe function f(x) = x(x + 3) e–x/2 satisfies all the conditions of Rolle's theorem in [–3, 0]. The value of c which verifies Rolle's theorem, is
For what values of a does the curve
f(x) = x(a2 – 2a – 2) + cos x is always strictly monotonic 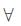 x ∈ R.
x ∈ R.
If the function f(x) = x3 – 6ax2 + 5x satisfies the conditions of Lagrange's mean theorem for the interval [1, 2] and the tangent to the curve y = f(x) at x = 7/4 is parallel to the chord joining the points of intersection of the curve with the ordinates x = 1 and x = 2. Then the value of a is
The function f(x) = tan-1 (sin x + cos x) is an increasing function in
A function y = f(x) has a second order derivative f" = 6(x – 1). If its graph passes through the point (2, 1) and at that point the tangent of the graph is y = 3x – 5, then the function is
If f(x) = [a sin x + b cosx] / [c sin x + d cos x] is monotonically increasing, then
If f(x) = 1 + x ln 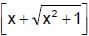 and g(x) =
and g(x) = 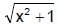 then for x ³ 0
then for x ³ 0
The set of values of the parameter `a' for which the function; f(x) = 8ax – a sin 6x – 7x – sin 5x increases & has no critical points for all x Î R, is
f : [0, 4] → R is a differentiable function then for some a, b Î (0, 4), f2(4) – f2(0) equals
Let f(x) = ax4 + bx3 + x2 + x – 1. If 9b2 < 24a, then number of real roots of f(x) = 0 are
If f(x) = (x – 1) (x – 2) (x – 3) (x – 4), then roots of f'(x) = 0 not lying in the interval
If f(x) = 1 + xm (x – 1)n, m, n ∈ N, then f'(x) = 0 has atleast one root in the interval
|
204 videos|290 docs|139 tests
|



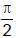 and f(a, b) =
and f(a, b) = 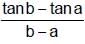 , then
, then
















