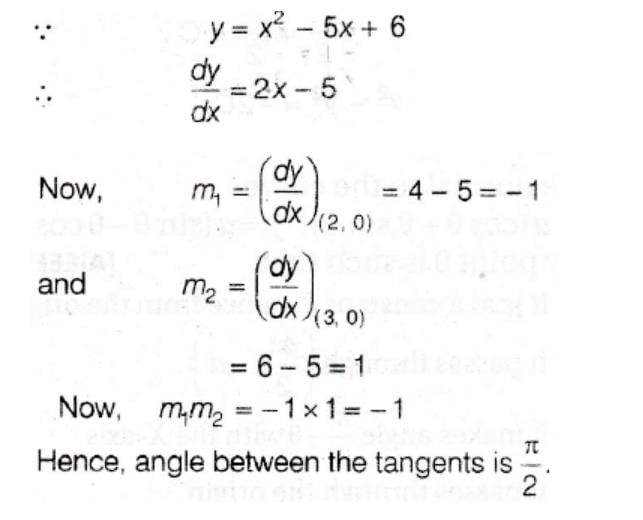JEE Advanced Level Test: Tangent & Normal- 1 - JEE MCQ
21 Questions MCQ Test Mathematics (Maths) Class 12 - JEE Advanced Level Test: Tangent & Normal- 1
The area of the triangle formed by the positive x–axis and the normal and the tangent to the circle x2 + y2 = 4 at (1, 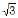 ) is
) is
Equation of the normal to the curve y = – 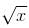 + 2 at the point of its intersection with the curve y = tan (tan–1 x) is
+ 2 at the point of its intersection with the curve y = tan (tan–1 x) is
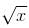 + 2 at the point of its intersection with the curve y = tan (tan–1 x) is
+ 2 at the point of its intersection with the curve y = tan (tan–1 x) isThe abscissa of the point on the curve ay2 = x3, the normal at which cuts off equal intercepts from the coordinate axes is
How many external tangents are there for two circles?
If curve y = 1 – ax2 and y = x2 intersect orthogonally then the value of a is
The coordinates of the point of the parabola
y2 = 8x, which is at minimum distance from the circle x2+(y+6)2=1 are
The length of the subtangent to the curve 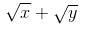 =3 at the point (4, 1) is
=3 at the point (4, 1) is
Water is poured into an inverted conical vessel of which the radius of the base is 2m and height 4m, at the rate of 77 litre/minute. The rate at which the water level is rising at the instant when the depth is 70 cm is: (use p = 22/7)
If the tangent at each point of the curve
y = x3 – 2ax2 + 2x + 5 makes an acute angle with the positive direction of x–axis, then
All points on the curve y2=4a at which the tangents are parallel to the axis of x, lie on a
A curve is represented by the equations, x = sec2 t and y = cot t where t is a parameter. If the tangent at the point P on the curve where t = p/4 meets the curve again at the point Q then |PQ| is equal to
The curves x3 + p xy2 = –2 and 3 x2y – y3 = 2 are orthogonal for
If curves = 1 and xy = c2 intersect orthogonally, then
The ordinate of y=(a/2) (ex/a + e–x/a) is the geometric mean of the length of the normal and the quantity
Angle between the tangents to the curve
y = x2 – 5x + 6 at the points (2, 0) and (3, 0) is
Water is being poured on to a cylindrical vessel at the rate of 1 m3/min. If the vessel has a circular base of radius 3m, the rate at which the level of water is rising in the vessel is
Find the number of points on the curve
x2 + y2 – 2x – 3 = 0 at which the tangents are parallel to the x-axis.
If at any point on a curve the subtangent and subnormal are equal, then the tangent is equal to
The number of values of c such that the straight line 3x + 4y = c touches the curve = x + y is
The points(s) of intersection of the tangents drawn to the curve x2y = 1 – y at the points where it is intersected by the curve xy = 1 – y is/are given by
|
204 videos|290 docs|139 tests
|



 is equal to
is equal to