JEE Advanced Level Test: Tangent and Normal- 2 - JEE MCQ
9 Questions MCQ Test Mathematics (Maths) Class 12 - JEE Advanced Level Test: Tangent and Normal- 2
The x–intercept of the tangent at any arbitrary point of the curve 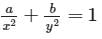 is proportional to
is proportional to
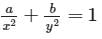 is proportional to
is proportional toThe line 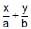 = 1 touches the curve y = be–x/a at the point
= 1 touches the curve y = be–x/a at the point
If the subnormal at any point on y = a1 – n xn is of constant length, then the value of n is
If the tangent at P of the curve y2 = x3 intersects the curve again at Q and the straight lines OP, OQ make angles a, b with the x–axis, where `O' is the origin, then tan a/tan b has the value equal to
The length of the normal to the curve x = a(q + sin q), y = a (1 – cos q), at q = is
The beds of two rivers (within a certain region) are a parabola y = x2 and a straight line y = x – 2. These rivers are to be connected by a straight canal. The co-ordinates of the ends of the shortest canal can be
If the area of the triangle included between the axes and any tangent to the curve xn y = an is constant, then n is equal to
For the curve x = t2 – 1, y = t2 – t, the tangent line is perpendicular to x-axis where
|
204 videos|290 docs|139 tests
|




















