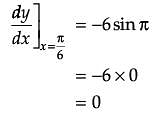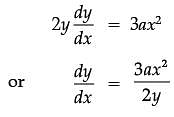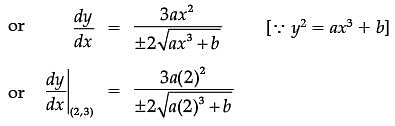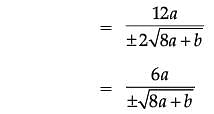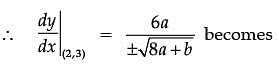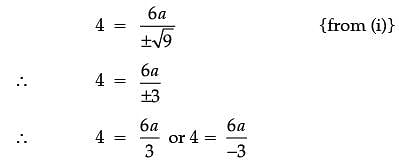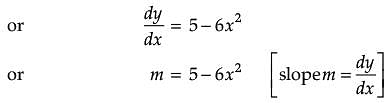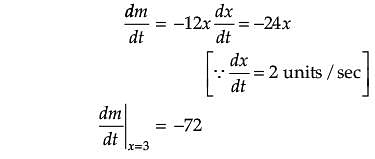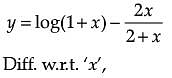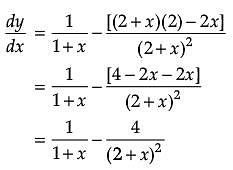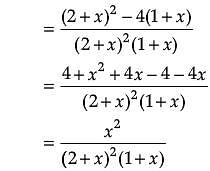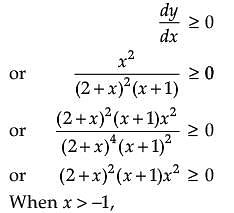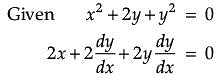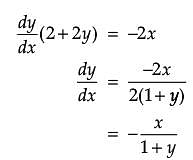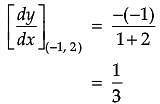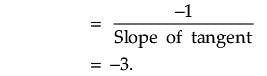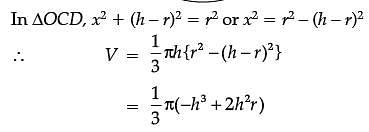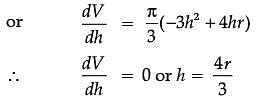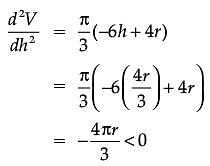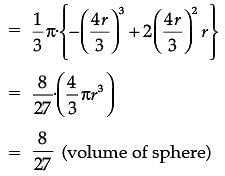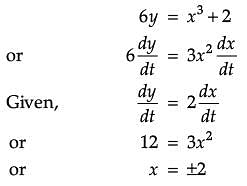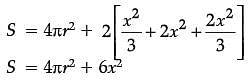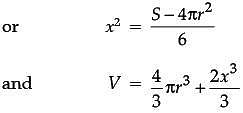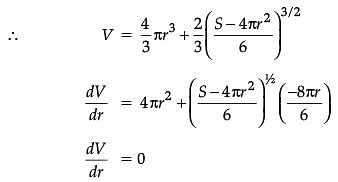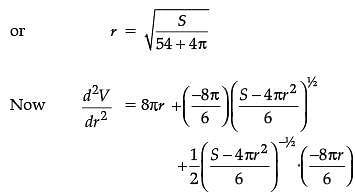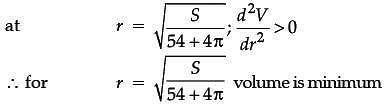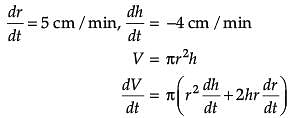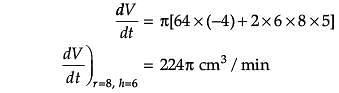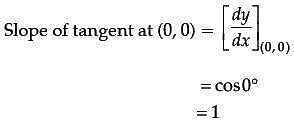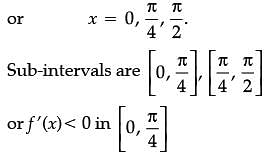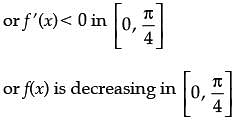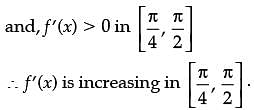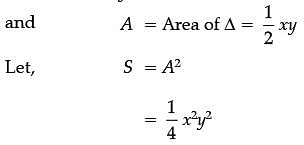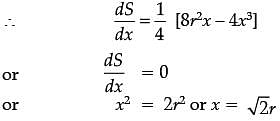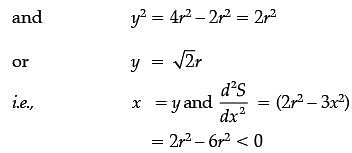Test: Application of Derivatives- Assertion & Reason Type Questions - JEE MCQ
15 Questions MCQ Test Mathematics (Maths) Class 12 - Test: Application of Derivatives- Assertion & Reason Type Questions
Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): At x = π/6, the curve y = 2cos2 (3x) has a vertical tangent.
Reason (R): The slope of tangent to the curve y = 2cos2 (3x) at x = π/6 is zero.
Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): The function y = [x(x – 2)]2 is increasing in (0, 1) ∪ (2, ∞)
Reason (R): dy/dx = 0, when x = 0, 1, 2
Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
The equation of tangent at (2, 3) on the curve y2 = ax3 + b is y = 4x – 5.
Assertion (A): The value of a is ±2
Reason (R): The value of b is ±7
Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
The total revenue received from the sale of x units of a product is given by R(x) = 3x2 + 36x + 5 in rupees.
Assertion (A): The marginal revenue when x = 5 is 66.
Reason (R): Marginal revenue is the rate of change of total revenue with respect to the number of items sold at an instance.
Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): The function f(x) = x3 – 3x2 + 6x – 100 is strictly increasing on the set of real numbers.
Reason (R): A strictly increasing function is an injective function.
Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): For the curve y = 5x – 2x3, if x increases at the rate of 2 units/sec, then at x = 3 the slope of curve is decreasing at 36 units/sec.
Reason (R): The slope of the curve is dy/dx
Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): The function ![]() is a decreasing function of x throughout its domain.
is a decreasing function of x throughout its domain.
Reason (R): The domain of the function
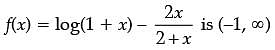
Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): The slope of normal to the curve x2 + 2y + y2 = 0 at (–1, 2) is –3.
Reason (R): The slope of tangent to the curve x2 + 2y + y2 = 0 at (–1, 2) is 1/3
Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
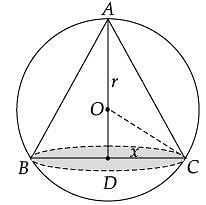
Assertion (A): The altitude of the cone of maximum volume that can be inscribed in a sphere of radius r is 4r/3.
Reason (R): The maximum volume of the cone is 8/27 of the volume of the sphere.
Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
A particle moves along the curve 6y = x3 + 2.
Assertion (A): The curve meets the Y axis at three points.
Reason (R): At the points (2,5/3) and (–2, –1) the ordinate changes two times as fast as the abscissa.
Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
The sum of surface areas (S) of a sphere of radius ‘r’ and a cuboid with sides x/3, x and 2x is a constant.
Assertion (A): The sum of their volumes (V) is minimum when x equals three times the radius of the sphere.
Reason (R): V is minimum when 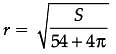
Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
The radius r of a right circular cylinder is increasing at the rate of 5 cm/min and its height h, is decreasing at the rate of 4 cm/min.
Assertion (A): When r = 8 cm and h = 6 cm, the rate of change of volume of the cylinder is 224p cm3/min
Reason (R): The volume of a cylinder is ![]()
Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): The equation of tangent to the curve y = sin x at the point (0, 0) is y = x.
Reason (R): If y = sin x, then dy/dx at x = 0 is 1
Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Consider the function f(x) = sin4x + cos4x.
Assertion (A): f(x) is increasing in 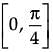
Reason (R): f(x) is decreasing in 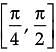
Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
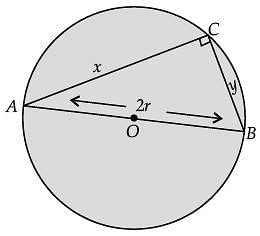
AB is the diameter of a circle and C is any point on the circle.
Assertion (A): The area of DABC is maximum when it is isosceles.
Reason (R): DABC is a right-angled triangle.
|
204 videos|290 docs|139 tests
|