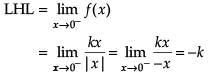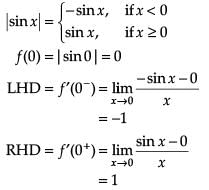Test: Continuity and Differentiability- Assertion & Reason Type Questions - JEE MCQ
8 Questions MCQ Test Mathematics (Maths) Class 12 - Test: Continuity and Differentiability- Assertion & Reason Type Questions
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion: If y = sin-1 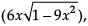 then
then 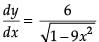
Reason: 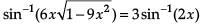
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion : |sin x| is continuous for all x ∈ R.
Reason : sin x and |x| are continuous in R.
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion : A continuous function is always differentiable.
Reason : A differentiable function is always continuous.
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion : f(x) = tan2 x is continuous at x = π/2
Reason : g(x) = x2 is continuous at x = π/2.
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion : f(x) = [x] is not differentiable at x = 2.
Reason : f(x) = [x] is not continuous at x = 2.
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Consider the function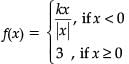 which is continuous at x = 0.
which is continuous at x = 0.
Assertion (A): The value of k is – 3.
![]()
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): |sin x| is continuous at x = 0.
Reason (R): |sin x| is differentiable at x = 0.
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Consider the function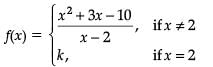
which is continuous at x = 2.
Assertion (A): The value of k is 0.Reason (R): f(x) is continuous at x = a, if
![]()
|
204 videos|290 docs|139 tests
|