Test: Inverse Trigonometric Functions- Assertion & Reason Type Questions - JEE MCQ
5 Questions MCQ Test Mathematics (Maths) Class 12 - Test: Inverse Trigonometric Functions- Assertion & Reason Type Questions
Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): sin-1(sin(2π/3)) = 2π/3
Reason (R): sin -1(sin θ) = θ, if q ∈ [(-π)/2, π/2]
Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): Principal value of cos–1(1) is π
Reason (R): Value of cos 0° is 1
Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): Range of tan–1x is [(-π/2, π/2)]
Reason (R): Domain of tan–1x is R.
Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): Range of cot–1 x is (0, π)
Reason (R): Domain of tan–1 x is R.
Directions : In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): Principal value of sin-1(1/√2) is π/4
Reason (R): Principal value of cot-1(-1/√3) is π/3
|
204 videos|290 docs|139 tests
|



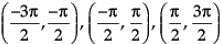 etc., is bijective and its range is R.
etc., is bijective and its range is R.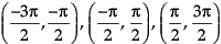 and soon.
and soon.