Test: Monotonicity - JEE MCQ
22 Questions MCQ Test Mathematics (Maths) Class 12 - Test: Monotonicity
The interval in which the function x3 increases less rapidly than 6x2 + 15x + 5 is
If y = (a + 2) x3 – 3ax2 + 9ax – 1 decreases monotonically 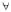 x ∈ R then `a' lies in the interval
x ∈ R then `a' lies in the interval
The true set of real values of x for which the function, f(x) = x ln x – x + 1 is positive is
The curve y = f(x) which satisfies the condition f'(x) > 0 and f"(x) < 0 for all real x, is
If the point (1, 3) serves as the point of inflection of the curve y = ax3 + bx2 then the value of `a' and `b' are
The function f(x) = x3 – 6x2 + ax + b satisfy the conditions of Rolle's theorem in [1, 3]. The value of a and b are
If f(x) =  ; g(x) =
; g(x) = 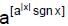 for a > 1, a ¹ 1 and x Î R, where {*} & [*] denote the fractional part and integral part functions respectively, then which of the following statements holds good for the function h(x), where (ln a) h(x) = (ln f(x) +ln g(x)).
for a > 1, a ¹ 1 and x Î R, where {*} & [*] denote the fractional part and integral part functions respectively, then which of the following statements holds good for the function h(x), where (ln a) h(x) = (ln f(x) +ln g(x)).
Given that f is a real valued differentiable function such that f(x) f'(x) < 0 for all real x, it follows that
f : R → R be a differentiable function x ∈ R. If tangent drawn to the curve at any point x ∈ (a, b) always lie below the curve, then
A value of C for which the conclusion of Mean Value Theorem holds for the function f(x) = loge x on the interval [1, 3] is
The function f(x) = x(x + 3) e–x/2 satisfies all the conditions of Rolle’s theorem in [–3, 0]. The value of c which verifies Rolle’s theorem, is
The number of values of `c' of Lagrange's mean value theorem for the function,
f(x) = (x – 1) (x – 2) (x – 3), x ∈ (0, 4) is
If f(x) and g(x) are differentiable in [0, 1] such that f(0) = 2, g(0) = 0, f(1) = 6, g(1) = 2, then Rolle's theorem is applicable for which of the following
Function for which LMVT is applicable but Rolle's theorem is not
|
204 videos|290 docs|139 tests
|


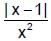 is monotonically decreasing in
is monotonically decreasing in

















