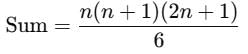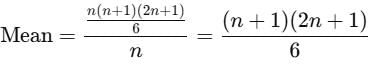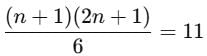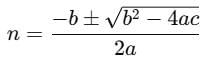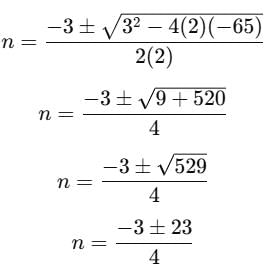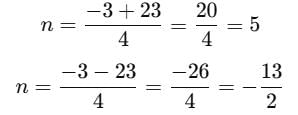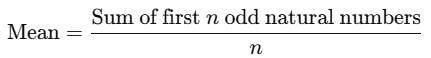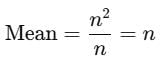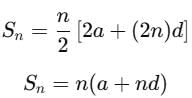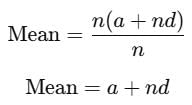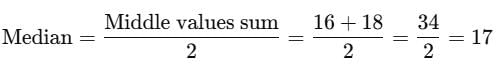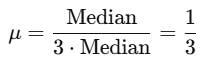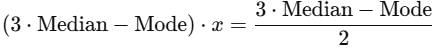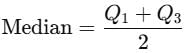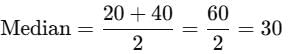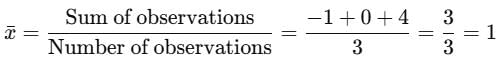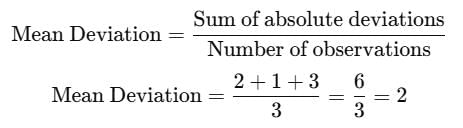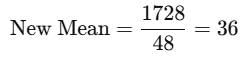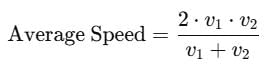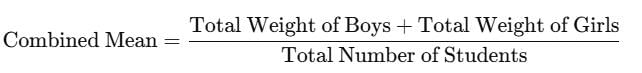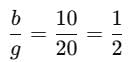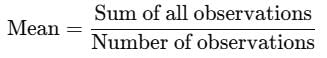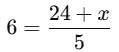Test: Statistics- 2 - Commerce MCQ
25 Questions MCQ Test Mathematics (Maths) Class 11 - Test: Statistics- 2
If the mean of the squares of first n natural numbers be 11, then n is equal to
If the mean of the first n odd natural numbers be n itself, then n is equal to
The mean of the first n terms of the A.P. (a + d) + (a + 3d) + (a + 5d) +………..is
If a, b, c be any three positive numbers, then the least value of (a + b + c) 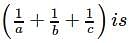
If the two lines of regression are at right angles, then ρ(X,Y) is equal to
If the two lines of regression are y = 3x – 5 and y = 2x – 4 , then ρ(X,Y) is equal to
Least square lines of regression give best possible estimates, when ρ(X,Y) is equal to
For a symmetrical distribution Q1 = 20 and Q3. = 40. The median of the data is
The range of the following set of observations 2,3,5,9,8,7,6,5,7,4,3 is
Which of the following, in case of a discrete data, is not equal to the median?
Mean deviation from the mean for the observations – 1, 0 ,4 is
The mean of 50 observations is 36, if two observations are 30 and 42 are deleted , then the mean of the remaining observations is
A man travels at a speed of 20 km/hour and then return at a speed of 30 km/hour. His average speed of the whole journey is
In a group of students, mean weight of boys is 80 kg and mean weight of girls is 50kg.If the mean weight of all the students taken together is 60kg, then the ratio of the number of boys to that of the girls is
|
75 videos|238 docs|91 tests
|