Test: Circles- 1 - SAT MCQ
10 Questions MCQ Test Mathematics for Digital SAT - Test: Circles- 1

In the given figure, the area of the smaller circle is A1 and the area of the bigger circle is (A1 + A2). If the radius of the smaller circle is 6cm and A2 = 3A1, find the radius of the bigger circle.
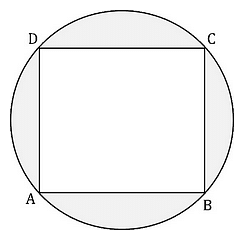
ABCD is a square inscribed in a circle. If the length of BC = 8cm. Find the area of the shaded region.
A circular track needs to be fenced along the inner and outer boundaries of the track to prevent stalkers from interrupting any events. What is the width of the track?
(1) The fencing used for the outer boundary can actually be used to fence the inner boundary twice.
(2) The area of the circle formed by the inner boundary is 10 sq. meter.
(2) The area of the circle formed by the inner boundary is 10 sq. meter.
A company X has offices in four locations – A, B, C and D. The figure above represents a circle graph of X’s profits from each of the four locations in April 2010. One-thirds of companies profits in were registered from B while one-fourths of its profits were registered from A. Were the profits from the location C of the company more than the profits from location D of the company?
(1) x > y
(2) The sum of the profits from A and D combined were larger than the sum of the profits from B and C combined.
The floor of a rectangular room of 72 square meters area needs to be covered by a circular carpet that occupies exactly half the area of the floor. What must be the circumference of the carpet in meters?
Little Johnny wants to eat a candy (circular in shape) using chopsticks! For this he makes sure that one end of either chopstick is touching the other (held in his hand) and the other end is used to hold the candy, as shown in the figure below. If his mom wants him to maintain a distance of at least 10 cm between his hands and his mouth while eating, what is the minimum length (in cm) of chopsticks required by him to eat the candy using chopsticks? (Assume that both the chopsticks are of equal length and that the radius of the candy is 6 cm.)
A man distributed his wealth among his wife and three sons such that his second son got twice the amount the eldest son received, his youngest son received twice the amount the second son got and his wife got twice the amount the youngest son received. If the man were to represent his wealth in a circle diagram, how many degrees of the circle must be allocated to represent the portion that the second son receives?
A square is inscribed in a big circle and a small circle is inscribed in the square as shown in the figure above. (All of them are concentric and their center is the point O). If the radius of the big circle is √2 cm, what is the semi perimeter of the small circle?
A bigger circle (with center A) and a smaller circle (with center B) are touching each other externally. PT and PS are the tangents drawn to these circles from an external point (as shown in the figure). What is the length of ST?
(1) The radii of the bigger and the smaller circles are 9 cm and 4 cm respectively
(2) PB = 52/5 cm
What is the area of the 144o sector of the circle?
(1) The square with one of the sides as the chord that subtends an angle of 90o on the circle measures 64 sq. cm. in area.
(2) When an isosceles triangle is constructed by taking the longest chord of the circle and the other vertex on the circumference of the circle, the length of each of the equal sides of the triangle is 4√2 cm.
|
185 videos|124 docs|75 tests
|