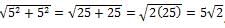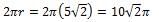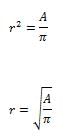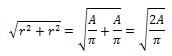Test: Circles- 2 - CAT MCQ
20 Questions MCQ Test Additional Study Material for CAT - Test: Circles- 2
The diameter of the tyres of a car is 63 centimetres. If the car is driven at a constant speed such that the tyre makes one 360-degree rotation in 0.24 seconds, what is the approximate speed of the car in kilometres per hour?
Point A lies on a circle whose center is at point C. Does point B lie inside the circle?
- BC2 = AC2 + AB2
- ∠CAB is greater than ∠ABC
The tyre of a car made an average of 500 revolutions per minute in a particular trip. If the radius of the tyre was 10 centimeters and the car was driven for 1 hour without any stoppages, approximately how much distance in kilometers was covered in the trip?
ΔABC, which is right-angled at B, is inscribed in a circle with centre O and radius 6 units. If the length of the smaller arc between points A and B is 4π units, what is the length of line segment BC?
In the figure above, triangle ABC is inscribed in the circle with center O, such that CD is perpendicular to AB. If the length of the side AC is centimeters, ∠AOB is 60o and the smaller perimeter of the sector AOB is 12 + 2π centimeters, what is the perimeter of the triangle ABC in centimeters?
In the given figure, AB and CD are the longest chords of the circle with their lengths equal to 8 units. If the length of the minor arc BC is 1/6th of the perimeter of the circle, what is the length of the chord BD?
If O is the center of the circle above and the length of chord AB is 2 units, what is the length of the arc ACB?
(1) The area of ΔOAB is √3 square units
(2) The area of sector OACBO is 2π/3
The annual money spent by a company on search engine marketing, content marketing and affiliate marketing is to be shown on a circlular graph. If the size of each sector of the graph is proportional to the amount of money it represents, did the company spend the most money on search engine marketing?
(1) The angle of the sector that represents content marketing is 80o
(2) The angle of the sector that represents affiliate marketing is 210o
The figure above shows a rectangular plot of land OPQR. In this plot, a patch of land OABO, where the path AB represents a circular arc of radius 20√2 metres, is developed as a lawn. The point A is at a distance of 20 metres each from sides OR and OP. The point B is at a distance of 10√6 metres from side OP and 10√2 metres from side OR. What is the area, in square metres, of the intended lawn?
A circle is inscribed in a square ABCD such that the circle touches all the sides of the square. If the perimeter of the shaded region is 24 + 6π, what is the area of the shaded region?
Two concentric circles have their centers at point O such that a line segment AB having its end points on the outer circle touches the inner circle at point C. The length of the line segment AB is times the radius of the inner circle. If an equilateral triangle is drawn such that the area of the triangle is equal to the ratio of the radii of the outer circle and the inner circle respectively, what is the length of the side of the triangle?
If a circle has the same area as right triangle PQR shown in the figure above. Which of the following is the closest in value to the radius of the circle?
In the figure above, triangle ABC is inscribed in a circle whose centre O has the x- and y-coordinates as (0,0). If the x- and y- coordinates of point A are (-4,0) and ∠BAC = 30∘, what is the area, in square units, of triangle AOB?
Lines CA and CB touch the circle only at points A and B respectively, as shown in the figure above. If the centre O of the circle is at the point (0,0), the coordinates of point C are (0,2) and the radius of the circle is √2 units, what are the coordinates of point A?
In the coordinate system, the center of a circle lies at (2, 3). If point A with coordinates (-1, 7) does not lie outside the circle, which of the following points must lie inside the circle?
I. (0, 7)
II. (5, -1)
III. (-2, 7)
15 children are given tags numbered from 1 to 15 and are seated in a circular formation in the increasing order of their respective tag numbers. The total area covered by the circular formation is 36π square units and the distance between any two neighbouring children in the formation is equal., If the number of children seated between the child with tag number m and the child with tag number 1 is equal to the number of children seated between the child with tag number m and the child with tag number 15, what is the minimum distance covered along the circular formation by the child with tag number 1 to reach the child with tag number m -2 and then go back to his original position?
The figure above shows a circle whose centre O has the x- and y- coordinates as (6,0). Points A(m,n) and B(8,2) are marked on the circle such that ∠AOB = 105∘. If the circle is symmetrical about the x-axis, what is the value of m?

If O is the center of the circle above, what fraction of the circular region is encompassed by an angle of x degrees?
In the coordinate plane, a circle has center (-1, -3) and passes through the point (4,2). What is the circumference of the circle?
The circle with center C shown above is tangent to both axes and has an area of A. What is the distance from O to C, in terms of A?
|
5 videos|378 docs|164 tests
|