Test: Lines & Angles - 2 - ACT MCQ
10 Questions MCQ Test Mathematics for ACT - Test: Lines & Angles - 2
In the given figure AB || CD, ∠A = 128°, ∠E = 144°. Then, ∠FCD is equal to :


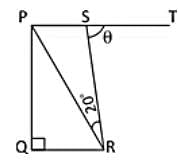
In the trapezium PQRS, QR || PS, ∠Q = 90°, PQ = QR and ∠PRS = 20°. If ∠TSR = θ, then the value of θ is:

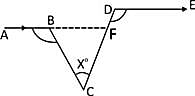
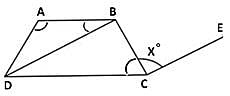
In the adjoining figure, ∠ABC = 100°, ∠EDC = 120° and AB || DE. Then, ∠BCD is equal to:

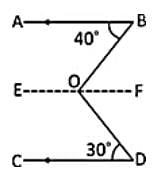
In the given figure, AB || CD, ∠ABO = 40° and ∠CDO = 30°. If ∠DOB = x°, then the value of x is:

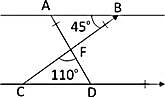
In the given figure, AB || CD, m∠ABF = 45° and m∠CFC = 110°. Then, m∠FDC is:
In the given figure, line CE is drawn parallel to DB. If ∠BAD = 110°, ∠ABD = 30°, ∠ADC = 75° and ∠BCD = 60°, then the value of x° is:
If two supplementary angles differ by 44°, then one of the angle is:
Consider the following statements
If two straight lines intersect, then
I. vertically opposite angles are equal.
II. vertically opposite angles are supplementary.
III. adjacent angles are complementary.
Which of the statements given above is/are correct?
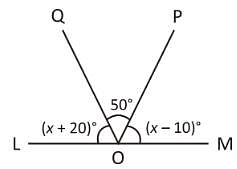
In the figure given above LOM is a straight line. What is the value of x°?
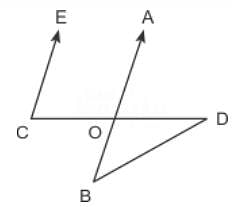
In the figure given above, EC is parallel to AB, ∠ECD = 70° and ∠BDO = 20°. What is the value of ∠OBD?
|
144 videos|100 docs|61 tests
|