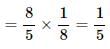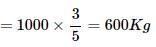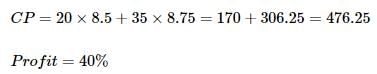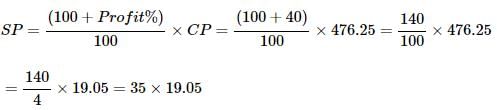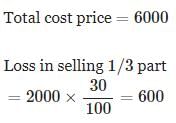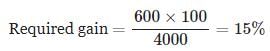Test: Mixtures- 2 - GMAT MCQ
15 Questions MCQ Test Quantitative for GMAT - Test: Mixtures- 2
A solution consists of only water and alcohol such that the ratio of alcohol to water in the solution is 7:3. How much amount of water should be added to the solution (in mililiters) so that the resulting solution contains 60% alcohol?
- Total quantity of the resulting solution is 350 mililiters.
- The original solution contains 10.5 mililiters of alcohol for every 4.5 mililiters of water.
Solution A contains equal amount of alcohol and water in it. It is heated till 50 percent of the water in solution A evaporates. Solution B, whose volume is equal to the reduced volume of water in Solution A, is then added to Solution A and the volume of alcohol in the resultant solution is equal to 12 liters. If solution B contains alcohol and water in the ratio 2:3, how many more liters of water should be added to the resultant solution to increase the concentration of water in the resultant solution to 50 percent?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Solution A is made up of alcohol and water mixed in the ratio of 21:4 by volume; Solution B is made up of alcohol and water mixed in the ratio of 2:3 by volume. If Solution A and Solution B are mixed in the ratio of 5:6 by volume, what percent of the resultant mixture is alcohol?
And using our inferences in the Given section, we can easily find the values of CB and CB and thus, answer the question.
A 20 kilograms mixture of dry fruits consisting of x percent of almonds is formed by mixing a kilograms of mixture A and b kilograms of mixture B. If mixture A consists of y percent of almonds and mixture B consists of 20% of almonds, what is the weight of almonds in kilograms in mixture A? Assume that each mixture has a uniform composition, that is, samples taken from any part in a mixture will have the same composition as the overall mixture.
(1) The amount of almonds in mixture B is three-fifths of the total weight of mixture A
(2) If the weight of the final mixture is reduced by 25 percent, the almonds in the final mixture would reduce by 1.5 kilograms
A salt-water solution that contains 8% salt by volume is kept in the sun till enough water evaporates from the solution such that the concentration of salt in the solution becomes 20%. If the volume of the remaining solution is 20 liters, what was the volume of the solution before it was kept in the sun?
A container consists of x liters of milk. The milk in the container is adulterated by adding water equal to 50 percent of the milk in
the container. If a person takes out 6 liters of the milk solution from the container, how many liters of water does he take out?
A solution contains ethanol, methanol and water in the ratio of 1:4:15 by volume. The composition of this solution is altered by adding ethanol, methanol and water such that the amount of ethanol per unit volume of methanol increases by 15 percentage points and the amount of water per unit volume of ethanol decreases by two-thirds. If the volume of the altered solution is 340 cubic units, which of the following is the volume, in cubic units, of methanol in the altered solution?
by 15 percent)
Packet A contains a mixture of salt and sugar and Packet B contains a mixture of salt and pepper. When the contents of the two packets are mixed in a bowl, the resultant mixture weighs 400 grams and contains 25% sugar. How many grams of salt are contained in Packet B?
(1) One-third of the mixture in Packet A is sugar
(2) 15% of the resultant mixture is pepper
A juice is made by mixing x liters of mango pulp with y liters of orange pulp and 14 liters of water where x and y are non-zero integers, mango pulp costs $6 per 10 liters and orange pulp costs $4 per 10 liters, is x >3?
(1) If water is available free of charge, the juice costs $1.6 per 10 liters
(2) If mango pulp had cost 20 cents more per liter, then the cost of the mango pulp used in the juice would have been more than $2 greater than the cost of the orange pulp used in the juice
A tea company sells two brands of tea leaves, Brand A and Brand B. Both the brands of tea leaves consist of three types of tea leaves, types-I, II and III, but in different weights. The cost of a kilogram of a brand of tea leaves is given by the expression $(100p+80q+50r), where p, q and r are the weights of type-I, II and III tea leaves respectively in 1 kilogram of that brand of tea leaves. Which of the two brands of tea leaves costs more?
(1) The individual percentage weights of type-I and type-III tea leaves are greater in Brand A than in Brand B
(2) The percentage weight of type-I tea leaves in Brands A and B is 40 percent and 20 percent respectively
A solution contains water, milk and liquid chocolate in the ratio of 2:3:5 by volume. If y liters of water and milk each are added to this solution, the resultant solution would contain 25 percent of water by volume. If the volume of this resultant solution is 120 liters, what is the value of y in liters?
A vessel is filled with liquid, 3 parts of which are water and 5 parts of syrup. How much of the mixture must be drawn off and replaced with water so that the mixture may be half water and half syrup?
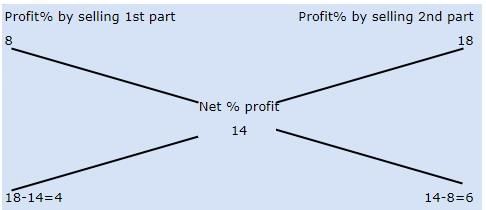
A merchant has 1000 kg of sugar part of which he sells at 8% profit and the rest at 18% profit. He gains 14% on the whole. The Quantity sold at 18% profit is
John bought 20 kg of wheat at the rate of Rs.8.50 per kg and 35 kg at the rate of Rs.8.75 per kg. He mixed the two. Approximately at what price per kg should he sell the mixture to make 40% profit as the cost price?
A butler stole wine from a butt of sherry which contained 32% of spirit and then replaced what he stole by wine containing only 18% spirit. The butt was then of 24% strength only. How much of the butt had he stolen?
|
110 videos|110 docs|120 tests
|
|
110 videos|110 docs|120 tests
|
Top Courses for GMAT
Important Questions for Mixtures- 2
Mixtures- 2 MCQs with Answers
Online Tests for Mixtures- 2 Quantitative for GMAT
|
© EduRev
|
Education Revolution
|
Follow Us
|
