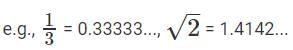Test: Sequence And Series - 2 - GMAT MCQ
15 Questions MCQ Test Quantitative for GMAT - Test: Sequence And Series - 2
If both 112 and 33 are factors of the number a * 43 * 62 * 1311, then what is the smallest possible value of 'a'?
How many different positive integers exist between 106 and 107, the sum of whose digits is equal to 2?
A number when divided by a divisor leaves a remainder of 24. When twice the original number is divided by the same divisor, the remainder is 11. What is the value of the divisor?
How many keystrokes are needed to type numbers from 1 to 1000?
When 242 is divided by a certain divisor the remainder obtained is 8. When 698 is divided by the same divisor the remainder obtained is 9. However, when the sum of the two numbers 242 and 698 is divided by the divisor, the remainder obtained is 4. What is the value of the divisor?
How many integral divisors does the number 120 have?
How many trailing zeros will be there after the rightmost non-zero digit in the value of 25!?
What is the remainder when 1044 * 1047 * 1050 * 1053 is divided by 33?
This data sufficiency problem consists of a question and two statements, labeled (1) and (2), in which certain data are given. You have to decide whether the data given in the statements are sufficient for answering the question. Using the data given in the statements, plus your knowledge of mathematics and everyday facts (such as the number of days in a leap year or the meaning of the word counterclockwise), you must indicate whether -
Q.
Is x3 > x2?
1. x > 0
2. x < 1
Numbers: All numbers used are real numbers.
This data sufficiency problem consists of a question and two statements, labeled (1) and (2), in which certain data are given. You have to decide whether the data given in the statements are sufficient for answering the question. Using the data given in the statements, plus your knowledge of mathematics and everyday facts (such as the number of days in a leap year or the meaning of the word counterclockwise), you must indicate whether -
Q. Is x/y a terminating decimal?
1. x is a multiple of 2
2. y is a multiple of 3
This data sufficiency problem consists of a question and two statements, labeled (1) and (2), in which certain data are given. You have to decide whether the data given in the statements are sufficient for answering the question. Using the data given in the statements, plus your knowledge of mathematics and everyday facts (such as the number of days in a leap year or the meaning of the word counterclockwise), you must indicate whether -
Q. Is the positive integer X divisible by 21?
1. When X is divided by 14, the remainder is 4
2. When X is divided by 15, the remainder is 5
This data sufficiency problem consists of a question and two statements, labeled (1) and (2), in which certain data are given. You have to decide whether the data given in the statements are sufficient for answering the question. Using the data given in the statements, plus your knowledge of mathematics and everyday facts (such as the number of days in a leap year or the meaning of the word counterclockwise), you must indicate whether -
Q. If x and y are positive integers, is y odd?
1. x is odd.
2. xy is odd.
This data sufficiency problem consists of a question and two statements, labeled (1) and (2), in which certain data are given. You have to decide whether the data given in the statements are sufficient for answering the question. Using the data given in the statements, plus your knowledge of mathematics and everyday facts (such as the number of days in a leap year or the meaning of the word counterclockwise), you must indicate whether -
Q. Is xy < 0?
1. 5|x| + |y| = 0
2. |x| + 5|y| = 0
This data sufficiency problem consists of a question and two statements, labeled (1) and (2), in which certain data are given. You have to decide whether the data given in the statements are sufficient for answering the question. Using the data given in the statements, plus your knowledge of mathematics and everyday facts (such as the number of days in a leap year or the meaning of the word counterclockwise), you must indicate whether -
Q. When a positive integer 'x' is divided by a divisor 'd', the remainder is 24. What is d?
1. When 2x is divided by d, the remainder is 23.
2. When 3x is divided by d, the remainder is 22
This data sufficiency problem consists of a question and two statements, labeled (1) and (2), in which certain data are given. You have to decide whether the data given in the statements are sufficient for answering the question. Using the data given in the statements, plus your knowledge of mathematics and everyday facts (such as the number of days in a leap year or the meaning of the word counterclockwise), you must indicate whether -
Q. How many of the numbers x, y, and z are positive if each of these numbers is less than 10?
1. x + y + z = 20
2. x + y = 14
|
115 videos|106 docs|113 tests
|